编译原理基础

Riicarus大约 76 分钟

编译原理基础

绪论
- 高级语言
- 强制式语言
数据类型
控制结构
- 语句级控制结构
- 单元级控制结构
程序语言的设计
- 形式语言
  - 术语
  - 文法
- 语言
编译概述
- 基本概念
- 编译步骤
词法分析
自上而下的语法分析
自下而上的语法分析
语义分析和中间代码生成
代码优化和目标代码生成
运行时存储空间的组织

绪论

高级语言

翻译高级语言的程序--编译程序/编译器

高级语言--编译器--机器码

高级语言:

直观, 自然, 易于理解
易读, 易写, 易于交流/出版和存档
一般独立于机器, 易于移植

强制式语言

语言分类:

强制式语言(命令式语言, 基于命令)
函数式语言(基于数学函数)
逻辑式语言(基于数理逻辑的谓词演算)
对象式语言(基于抽象数据类型)

语言发展:

第一代语言(机器语言, 依赖于机器指令系统)
第二代语言(汇编语言, 机器语言的符号化)
第三代语言(通常的高级语言, 命令式语言)
第四代语言(说明性语言, 告诉机器做什么)
新一代语言(理论基础和风格与高级语言不同, 函数式/逻辑式语言)

强制式语言的基础: 冯-诺伊曼体系结构

冯-诺伊曼体系结构的特点:

数据或指令以二进制形式存储
使用存储程序的工作方式(程序要执行必须先存储到存储器中)
程序顺序执行
存储器的内容可以被修改

冯-诺伊曼模型在高级语言中的呈现形式:

变量: 存储单元由变量的概念来代替, 可以代表一个或者一组单元, 可以修改(变量是存储的抽象, 存储不仅存储指令, 还会存储数据)
赋值: 计算结果必须存储(赋值是对存储器的内容进行修改)
重复: 语句顺序执行, 指令存储在有限的存储器中, 完成复杂计算必须重复执行某些指令序列(循环语句)

高级语言的特征:

绑定(binding): 实体与其属性建立联系的过程

实体在声明(创建)的时候未必含有属性, 可能在编译或执行的时候才会明确指定实体的类型或属性.
一个实体在什么时候拥有什么样的属性, 是一个很重要的时间节点.

binding 的概念:

描述符: 编译程序中用来描述实体属性的表格的统称, 是实体到属性的映像.
静态绑定: 在编译时能确定的属性, 成为静态属性. 如果绑定在编译时完成, 运行时不改变, 称为静态绑定.
动态绑定: 实体的某些属性在运行时才能确定的属性. 绑定在运行时完成, 称为动态绑定.

在编译中, 静态仅指在编译时能确定的信息; 动态仅指运行时才能确定的信息.
如: 动态数组和静态数组

变量:

冯-诺伊曼体系结构在高级语言中最重要的特性.

变量是一个或若干个存储单元的抽象. 赋值语句是修改存储单元内容的抽象.

变量属性:

名称
作用域(空间概念)
- 静态作用域绑定: 按照程序语法结构静态地定义变量的作用域
- 动态作用域绑定: 按照程序的执行动态地定义变量的作用域
生存期(时间概念)
- 数据对象: 存储区和它保存的值
- 分配: 变量获得存储区的活动
值: 变量所对应存储区单元的内容
- 匿名变量的访问通过指针实现
- 变量与它的值的绑定是动态的
- 符号常数的值不能修改
- 变量的初始化, 几种处理方法:
  - 不初始化则出错
  - 随机
  - 缺省值 0
类型: 与变量相关联的值的类
- 可以用来解释变量绑定的存储区的内容的意义
- 语言定义时, 类型名通常绑定于某一个值类和某一组操作
- 语言实现是, 值和操作绑定于某种机器的二进制表示及机器指令

虚拟机: 由软件实现的机器

程序单元(Program Unit): 程序执行过程中的独立调用单位. 若干个编译好的单元结合起来, 组成一个完整的可执行程序.

活动记录: 存储程序单元正常运行所需的所有信息.

数据类型

引言--数据类型

数据类型是对存储器中所存储的数据进行的抽象. 包含了一组值的集合和一组操作.

数据类型的作用:

实现了数据抽象: 不需要关注数据的底层实现.
是程序员从机器的具体特征中解脱出来.
提高了编程效率.

数据类型的分类:

内部类型(build-in): 语言定义的
自定义类型(user-define): 用户定义的. 使用更多, 更重要.

内部类型

内部类型的特点:

反映基本硬件特性(不同类型的机器指令不同).
在语言级, 内部类型标志共用某些操作的数据对象的抽象表示(值 + 操作的数据对象的抽象).

内部类型的优势:

基本表示的不可见性.
编译时, 能检查变量使用的正确性.
编译时, 可以确定无二义的操作(整形的加法和浮点型的加法不同).
可以进行精度控制.

用户定义的类型

笛卡尔积

在高级语言中, 笛卡尔积数据类型通常体现为记录或者结构, 由若干个域组成, 每个域有一个唯一的名字. 一般用域名来选取域, 对其进行修改.

有限映像

从定义类型 DT(domain type) 的值的有限集合, 到值域类型 RT(range type) 的值的有限集合的函数称为有限映像.

在高级语言中, 通常体现为数组构造.
值域对象通过下标选取.
下标越界会出错, 动态检查.
下标可以用于选取值域的多个元素.
某些语言允许值域中的元素不是同一类型.
DT 到相应值的特定子集的绑定策略:
- 编译时绑定: 静态数组
- 对象建立时绑定: 执行到分程序时, 动态数组
- 对象处理时绑定: 子集范围可变

序列

序列由任意多个数据项组成, 这些数据项称为该序列的成分, 且类型相同, 记为 CT.

在高级语言中, 序列的体现是字符串和文件.
序列和有限映像的区别在于序列长度是无限的.

递归

如果数据类型包含属于同一类型 T 的成分, 那么类型 T 称为递归类型.

允许在类型定义中使用被定义类型的名字
指针是建立递归数据类型的重要手段

判定或

判定或是一种选择对象结构的构造机制, 规定在两个不同选择对象之间做出适当的选择; 每一个选择对象结构称为变体.

域数量或者类型都可能发生变化.

幂集

类型 T 的元素所有子集的集合, 称为幂集. 记为 Powerset(T), T 为基类型.

幂集类型的基本操作是集合的操作.

PASCAL 语言数据类型结构

PASCAL 非结构类型

内部类型: integer, real, boolean, char
有序类型: 每一个元素都有唯一的前驱和后继(可以进行比较), 如: 整形, 布尔型, 字符型
定义新的有序类型的方法
- 枚举型: 其值不能直接读写.
- 子界型: 动态检查范围.

PASCAL 聚合构造

数组构造: 构造符 ARRAY 允许定义有限映像; 数组构造一般形式: array[t1] of [t2]. t1 指定义域的类型, t2 为值域的类型.

var arr1 = [1..50] of integer
var arr2 = [1..70] of integer

PASCAL 记录构造

使用构造符 record 来定义笛卡尔积:

record field_1:type_1;
       field_2:type2;
       ...
       field_n:type_n;
end

也可以由变体记录(判定或的体现)

可以使用 . 来访问记录中的域.

PASCAL 文件构造

PASCAL 文件是任意类型的多个元素的序列
只能顺序处理
只能进行 PUT 和 GET 操作

PASCAL 指针

指针是 PASCAL 的第三类数据类型, 是非结构的, 可以用来构造递归结构.

指针可引用匿名数据对象, 这类对象由建立语句 NEW 显示分别配在堆上.
空指针的值是 nil
指针的操作: 赋值, 比较
PASCAL 指针只能指向匿名数据对象, 不能指向在堆栈上分配的单元.

C 语言数据类型结构

C 非结构类型

内部类型
用户自定义类型
非结构内部类型有整形, 实型(浮点型)和字符型.

C 用户自定义的非结构类型

即枚举类型

C 聚合构造

数组:
- 有限映像的体现.
- 按行存放(编译程序如何计算数组元素的位置).
- 对数组名的处理相当于指针.
结构
- 使用 struct.
- 支持笛卡尔积.
- 结构的各成员依次存放.
- 结构体可以嵌套.
联合
- 使用 union
- 支持判定或.
文件
- 只能是一个字符序列.
- 分为 ASCII 码文件和二进制文件.
- 支持顺序读写和随机读写
指针
- 指针是 C 的基础, 是第三种数据类型, 是非结构类型.
- 可以用来构造结构类型.
- 支持递归.
空类型
- void.
- 是非结构类型.

抽象数据类型

用户定义类型的基本表示和操作对外界可见, 不能很好的重用.
如何提供更好的抽象来达到信息隐蔽/重用的目的?

抽象数据类型的定义:

满足以下两点的用户定义类型称为抽象数据类型:

在实现该类型的程序单元中, 建立与表示有关的基本操作.
对使用该类型的程序单元来说, 该类型的表示是隐蔽的.

如: Java 中的 Class/Interface

类型检查

对数据对象的类型和使用的操作是否匹配的一致性检查称为类型检查.
语言的类型检查分为静态检查和动态检查.
- 静态检查使程序更有效.
- 动态检查使程序更方便, 但影响了可读性, 且降低执行效率.
语言按类型分类:
- 无类型语言.
- 弱类型语言(一部分类型检查在运行时完成).
- 强类型语言.

类型转换

将一个类型的值转换为另一个类型的值.
分为:
- 拓展(int -> long).
- 收缩(long -> int).
有些语言中, 类型转换的要求和规则是隐式的, 由编译程序自动生成(如 Java), 有一些是显示的(如 Go).
一般来说, 语言对基本类型提供适当的类型转换, 对复合类型或用户自定义类型不提供转换.
收缩可能导致信息丢失.

类型等价

什么时候两个类型可以相互赋值? ==> 等价类型.

等价类型:

名字等价: 完全由结构名字决定.
结构等价: 由类结构决定.

Go 是名字等价的:

type Void interface{}

var void Void = Void{}
var interfaceArg = interface{}

void != interfaceArg // true

实现模型

数据类型如何在编译程序中得到体现?
编译过程中, 数据类型在内存中如何表示?

在数据类型的实现模型中, 数据类型 = 描述符 + 数据对象. 描述符用来描述数据对象的所有属性.

内部类型和用户定义的非结构类型的实现模型

描述符一般由"类型"和一个指针组成.

结构类型的实现模型

笛卡尔积
- 各成分顺序排列.
- 描述符包含:
  - 类型名
  - 构造符
  - 若干三元式, 每个域对应一个三元式
有限映像
- 为每一成分分配整数个可编址的存储单元.
判定或
- 分配的空间要足以容纳需要最大空间的变体的值.

控制结构

程序员用来规定各个成分执行流程地控制机制 -- 控制结构. 这里主要讨论语句级控制结构和单元级控制结构.

语句级控制结构

语句级控制结构分为三种:

顺序(sequencing)
选择(selection)
重复(repetition)

顺序

一般使用 ; 或换行符作为顺序运算符.

选择

if 语句, if, else if, else. 可以搭配 begin, end, 也可以直接使用最近匹配原则来避免选择结构的二义性问题.
多重选择: 使用 select, case 或者 switch 结构.
Dijkstra 选择结构: 对非确定性的抽象.

循环

计数器制导: 当预先知道循环次数时, 在循环计数器值的有限集合上重复.
条件制导: 预先不知道循环次数, 使用条件制导重复结构, 条件通常是一个布尔表达式.

语句级控制结构分析

都来自冯.诺伊曼机的程序计数器的基础.

顺序, 选择, 重复都是对程序计数器操作的抽象.
goto 是对任意修改程序计数器的抽象

单元级控制结构

规定程序单元之间控制流程的机制.

显式调用
异常处理
协同程序
并发单元

显式调用

调用方式: 调用语句使用被调用单元的名称来进行调用; 调用语句将控制转向被调用单元, 被调用单元执行完后, 将控制返回调用单元.
参数传递: 参数的两种绑定方式
- 位置绑定
- 关键字绑定
副作用: 对局部环境的修改
- 降低程序可读性
- 限制数学运算律的使用
- 影响目标代码的优化
解决方式:别名
别名的影响:
- 可能带来严重程序问题
- 影响编译器优化

隐式调用

调用方式: 隐式的将控制从一个单元转向到另一个单元, 通常用于异常处理.
异常: 导致程序正常执行终止的事件, 要靠发送信号来引发. 用异常条件来表示, 并发出相应的信号, 引发相应的程序.
异常处理要考虑的问题:
- 异常如何说明? 作用域是什么?
- 异常如何发生?(如何发送信号?)
- 发出异常信号时, 如何控制要执行的单元?
- 发出异常时, 如何绑定相应的异常处理程序?
- 处理异常之后, 控制流程转向何处?

协同程序

协同程序: 实现两个或者两个以上的程序单元之间交错执行的程序称为协同程序.

如: 有程序单元 U1, U2, U1 开始执行, 执行到 resume U2 时, 显式激活 U2, 保存 U1 的现场, 将控制转向 U2 的执行点; 如果 U2 执行到 resume U1 时, 保存 U2 的现场, 将控制转到 U1 的执行点.

并发单元

并发性: 多个进程的执行概念上是可以重叠的, 当一个进程尚未终止, 但是另一个进程可能开始执行.

竞争: 进程之间通过竞争来得到共享的资源.

合作: 进程之间通过合作来达到共同的目的.

语言为实现进程之间的同步, 会提供同步语句(或称为同步原语)来实现进程间的通信.

不同的同步方式:

信号量
管程
会合

信号量有如下缺点:

简单低级, 难设计和理解
不能做静态检查
容易出错, 导致死锁

程序语言的设计

形式语言

术语

字母表: 字符的有限集合, 一般用 $\varSigma$ 表示. 其中的元素称为字母.
空串: 用 $\epsilon$ 表示, $\{\epsilon\}$ 表示仅包含空串的集合.
空集: 用 $\emptyset$ 表示.
如果 $\alpha$ 和 $\beta$ 是两个字符串, 则 $\alpha\beta$ 表示两者的连接.
如果 $A$ 和 $B$ 是两个字符串的集合, 那么 $AB$ 表示两者的连接, 即 $A$ , $B$ 中所有字符串的连接的集合.
闭包: $A^* = A^0 \cup A^1 \cup ... \cup A^n$

例: $\alpha = a_1a_2...a_n, \beta = b_1b_2...b_m$ , 则 $\alpha\beta = a_1a_2...a_n b_1b_2...b_m$

文法

文法 $G$ 定义为一个四元式:

$G=(V_T, V_N, S, P)$

其中:

$V_T$ : 终结符的集合
$V_N$ : 非终结符的集合
$S\in V_N$ : 开始符号
$P$ : 产生式的非空有限集

产生式: 一般写为 $\alpha \to \beta$ , 其中:
$\left\{ \begin{array}{l} \alpha \in V^*V_N V^* \\ \beta \in V^* \\ V = V_N \cup V_T \end{array} \right.$

语言

程序设计语言: 描述计算机所执行的算法的形式表示, 由两个部分组成:

语法: 用以构造程序机器成分的一组规则的集合.
- 生成的观点: 用一组规则生成一个语言.
- 识别的观点: 用一个机制来识别一个语言.
语义: 用以规定语法正确的程序或其成分的含义的一组规则的集合.

语法:

字母表: 语言允许使用字符的集合, 其元素为字符; 有字符组成的有限串(字符串)称为符号.
字汇表: 有符号组成的集合, 其元素为字.
词法规则: 规定什么样的字符串可以构成语言的有效符号.
语法规则: 规定一个顾好序列是否为一个字句, 并提供字句的结构(即: 什么样的符号序列是合法的).

编译概述

基本概念

翻译: 将一种语言编写的程序转换成完全等效的另一种语言编写的程序的过程称为编译. 在计算机中, 翻译由一个程序来实现, 称为翻译程序.
编译: 将高级语言程序翻译成低级语言程序; 实现编译的程序称为编译程序或编译器.
汇编程序: 将汇编语言程序翻译成机器语言的程序.
宿主语言: 编写编译程序的语言称为宿主语言; 源语言/目标语言/宿主语言通常是不同的语言.
如果一个编译程序能生成可供其宿主机执行的机器码, 则称该编译程序为自驻留的(self-resident).
如果编译程序是用源语言编写的, 则称该编译程序是自编译的(self-compiling).
如果一个编译程序生成的不是其宿主机的机器代码, 则成为交叉编译(cross-compiling).
解释: 不将源程序翻译成目标程序, 而是一边分析, 一边执行, 这种编译方法称为解释; 实现解释的程序, 称为解释程序(interpreter).
- 适合动态语言和交互式程序.
- 重复执行语句需要重新解释, 效率更低.

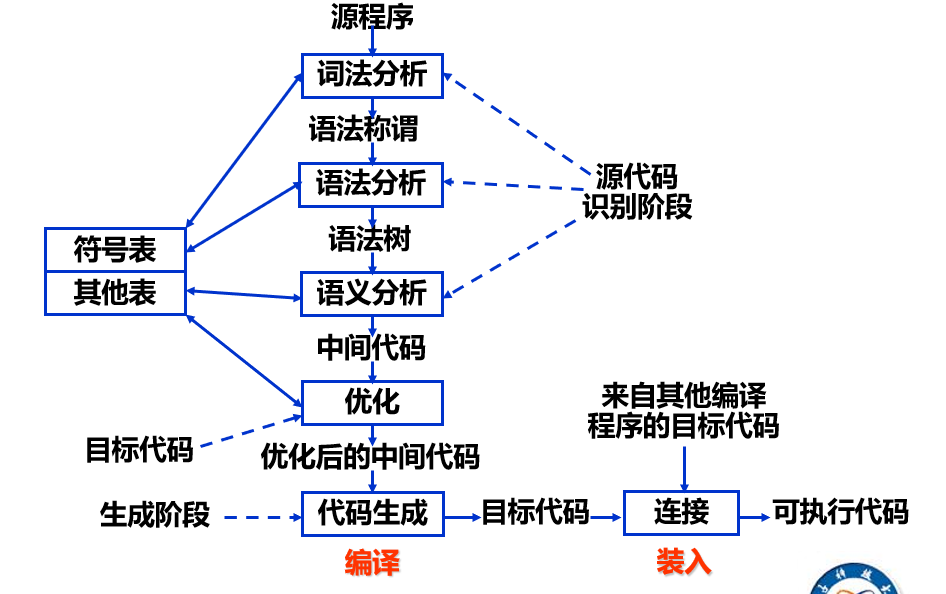
编译步骤

词法分析: 从左向右扫描源程序, 进行分析, 识别出符合此法规则的单词符号(token); 如果出错, 给出出错信息. (如: 基本字, 标识符, 常数, 运算符, 界符等)
语法分析: 对由此番分析识别出来的符号流, 按语法规则进行分析, 识别出语法单位, 给出语法树; 如果出错, 给出出错信息. (如: 表达式, 短语, 字句, 句子和子程序等)
语义分析: 按照语义要求对各种语法单位进行翻译; 大多数编译器采用中间语言来描述程序的语义. (并不直接翻译成机器码)
优化: 对中间代码进行一些等价变换, 使生成的目标程序效率更高.
目标代码生成: 将中间代码转换成目标代码.
符号表管理: 符号表存储程序中各种数据对象和实体的属性, 编译程序负责对这些表格进行创立和维护. 从语法分析步骤开始, 就需要符号表来进行辅助.
出错处理: 编译程序对发现的错误进行报告或相关处理.

词法分析

词法分析概述

词法分析器的功能:

从左到右逐个字符扫描源程序的字符流，分析出一个个单词符号，把由字符串表示的源程序转换成由符号串组成的串，供语法分析器使用；并对识别过程中发现的错误，输出有关信息.

理论上的词法分析器和语法分析器的关系:

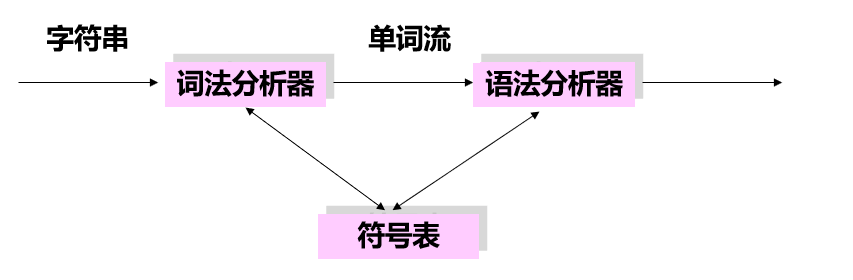
实际使用中的词法分析器和语法分析器的关系:

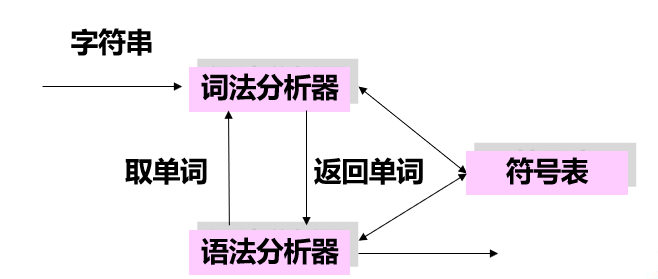
虽然两种关系不同, 但是没有改变词法分析器的作用, 即从字符串种分析出单词符号序列, 提供给语法分析器使用.

注意词法分析器也会使用符号表.

单词符号的类别

语言符号通常分为 5 种:

基本字: 语言预定义的具有特定含义的字符串, 也成为关键字或者保留字.
标识符: 用来作为实体的名字或语句标号, 通常是一个以字母开头的字母数字串.
常数: 包含各种类型的常数.
运算符: 包括算数/关系/逻辑运算符.
界符: 在程序中起分隔作用的符号, 如: ;, ,, ().

词法分析器的输出形式

词法分析器的输出通常为二元式: (单词的类别, 单词的属性).

当一个类别中有多于一个符号时, 存放符号自身的值到单词的属性中, 实际为指向符号表的指针.

类别编码的一般方式:

对于界符和运算符: 一符一类, 一个符号对应一个编码.
标识符: 作为单独的一类, 用自身的值区别不同的标识符.
对于常数: 按照类型编码, 按自身的值来区别不同的常数.
基本字: 一符一类.

例:
扫描语句: int i = 0, sum = 0;, 其输出为:
(int 的编码, -)
(标识符的编码, i 在符号表中的位置)
(= 的编码, -)
(整型常数的编码, 0 在常数表中的位置)
(, 的编码, -)
(标识符的编码, sum 在常数表中的位置)
(= 的编码, -)
(整型常数的编码, 0 在常数表中的位置)
(; 的编码, -)

词法分析器的设计

状态转换图: 是一张有限方向图, 由如下成分构成:

节点: 圆圈表示节点, 代表状态(双圈表示终态, 或者称为识别态);
有向边: 连接节点, 边上的标记字符表示该状态下可能接收或者识别的字符;

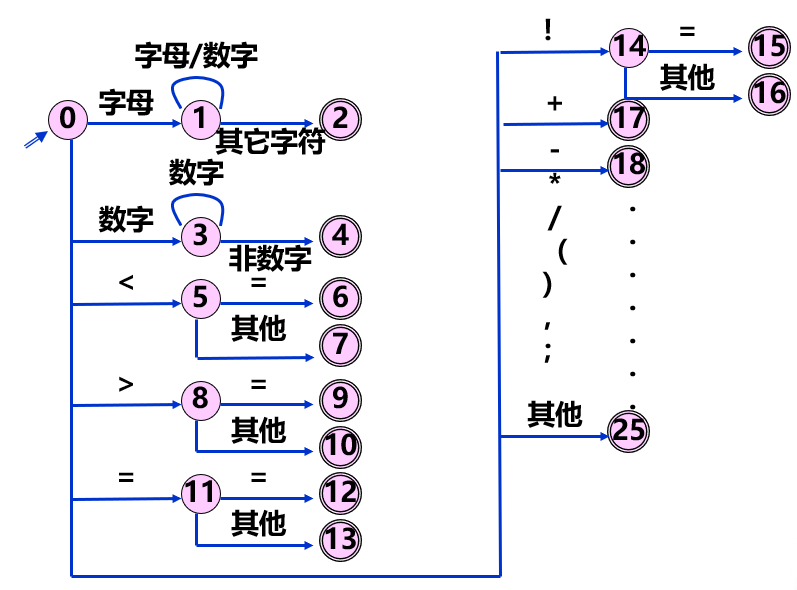
需要注意: 如果多读入了一个字符才确定终态, 需要回退一个字符. 如上图中的 7, 10, 13 等状态.

从状态转换图到词法分析器:

每个状态对应一段程序.
分支较多可以使用 case 语句.
回路使用 while 或者 if 语句.

符号表

用来记录程序中的各种符号的名字和相应属性的表格称为符号表.

符号表的内容:

程序中用户定义的各种数据对象的名字.
名字的种属.
名字的数据类型.
为名字分配的存储地址.
编译中的一些特征标志.

符号表的组织方式:

使用间接表技术, 名字使用指针进行表示, 不受大小限制, 便于整齐组织符号表.

常用的符号表结构:

线性表
散列表

自上而下的语法分析

引言--自上而下的语法分析

语法分析器的功能:

对经过词法分析得到的符号串, 按文法规则进行判断, 看它是否构成正确的句子. 如果是不正确的句子, 给出准确的错误信息, 并给出相应的处理; 如果是正确的句子, 给出其语法树.

错误信息对语言使用者非常重要, 越详细越好.

对于给定的文法 $G = (V_T, V_N, S, P)$ 以及输入串 $w \in V_T^*$ , 自上而下的语法分析: 从开始符号 $S$ 出发, 看能否找到一个最左推导, 使得 $S \Rightarrow w$ ; 或从 $S$ 出发, 能否构成一个语法树, 使得树的叶节点自左向右构成 $w$ .

回溯分析法

从文法的开始符号 $S$ 出发, 选取 $S$ 的候选式进行推到, 按最左推导进行下去. 如果推导失败, 再换用其他的候选式; 若穷尽所有的候选式都失败, 则表明 $w$ 不是 $G$ 的句子, $w$ 存在语法错误.

例: 有文法 $S \to xAy, A \to ab \mid a$ , 输入串为 $xay$ , 其自上而下分析过程为:
BackAnalysisProcess
左侧的推导无法匹配, 进而寻找右侧的, 能够匹配, $w$ 是 $G$ 的句子.

回溯的效率很低, 有没有不使用回溯的方式呢?
我们先来研究一下产生回溯的原因:

产生回溯的原因

文法含有公共左因子. 如: $A \to \alpha\beta_1 \mid \alpha\beta_2$ , 匹配串 $\alpha$ .

文法含有左递归. 如: $S \to Sa \mid b$ , 匹配串 $baa$ .

文法中含有 $\epsilon$ 产生式. 如:

\left\{ \begin{array}{l} S \to aAS \\ S \to b \\ A \to bAS \\ A \to \epsilon \\ \end{array} \right.

对串 $ab$ 进行推导.

回溯带来的问题:

如果产生式有多个候选式, 选择是盲目的.
如果文法存在左递归, 存在无限循环的可能.
回溯会导致空间和时间的大量消耗.
如果输入的语句有错误, 算法无法指出确切的位置.

消除回溯的方法

提取产生式的公共因子:

将文法

\left\{ \begin{array}{l} S \to xAy \\ A \to ab \mid a \\ \end{array} \right.

改造为

\left\{ \begin{array}{l} S \to xAy \\ A \to aB \\ B \to b \mid \epsilon \end{array} \right.

注意: 对公共因子的提取不能改变原有文法.

一般方法:

对产生式: $A \to \alpha\beta_1 \mid \alpha\beta_2 \mid ... \mid \alpha\beta_n \mid \gamma$

提取公共左因子: $\alpha$ ,

得到等价的产生式:

\left\{ \begin{array}{l} A \to \alpha B \mid \gamma \\ B \to \beta_1 \mid \beta_2 \mid ... \mid \beta_n \\ \end{array} \right.

消除直接左递归:

将左递归的产生式改写成等价的右递归的产生式.

对产生式: $I \to IL \mid ID \mid L$

改写为:

\left\{ \begin{array}{l} I \to LI' \\ I' \to LI' \mid DI' \mid \epsilon \\ \end{array} \right.

以上公式中, $I$ 表示 identifier(标识符), $L$ 表示 letter, $D$ 表示 digit.

一般的, 对产生式: $A \to A\alpha_1 \mid A\alpha_2 \mid ... \mid A\alpha_n \mid \beta$

改为:

\left\{ \begin{array}{l} A \to \beta A' \\ A' \to \alpha_1A' \mid \alpha_2A' \mid ... \mid \alpha_nA' \mid \epsilon \\ \end{array} \right.

消除间接左递归:

将文法 $G$ 的所有非终结符按任意序列排序, 设为 $A_1, ..., A_n$

执行以下算法, 消除可能的左递归:

for i := 1; i <= n; i++ {
    for j := 0; j < i - 1; j++ {
        // treat
    }
}

化简, 删除多余的产生式.

上述算法中, treat 部分逻辑如下:

把一个形如 $A_i \to A_j\alpha$ 产生式改写为 $A_i \to \gamma_1\alpha \mid \gamma_2\alpha \mid ... \mid \gamma_k\alpha$ , 其中 $A_j \to \gamma_1 \mid \gamma_2 \mid ... \mid \gamma_k$ 是 $A_j$ 的所有产生式;

消除 $A_i$ 产生式的直接左递归.

注意: 以上的算法不允许 $G$ 中包含 $\epsilon$ 产生式, 如果有, 需要先消除.

递归下降分析法

当文法改造为无公共左因子, 无左递归时, 让每个非终结符对应一个过程,该过程对相对应的非终结符产生式的右部短语进行语法分析, 这种分析方法称为递归下降分析法. 这样的分析器叫做递归下降分析器.

例: 对于文法 $G_1$ :

\left\{ \begin{array}{l} E \to T \mid E + T \\ T \to F \mid T*F \\ F \to (E) \mid i \\ \end{array} \right.

消除左递归后, 得到 $G_1'$ :

\left\{ \begin{array}{l} E \to TE' \\ E' \to +TE' \mid \epsilon \\ T \to FT' \\ T' \to*FT' \mid \epsilon \\ F \to (E) \mid i \end{array} \right.

对应的文法分析器如下:

func E() {
    T()
    EP()
}

func EP() {
    if sym == '+' {
      // 将词法 token 指针向后移动一位
      advance()
      T()
      EP()
    }
}

func T() {
    F()
    TP()
}

func TP() {
    if sym == '*' {
        advance()
        F()
        TP()
    }
}

func F() {
    if sym == 'i' {
        advance()
    } else if sym == '(' {
        advance()
        E()
        if sym == ')' {
            advance()
        } else {
            error()
        }
    } else {
        error()
    }
}

对串 $i+i*i$ 的处理过程如下:

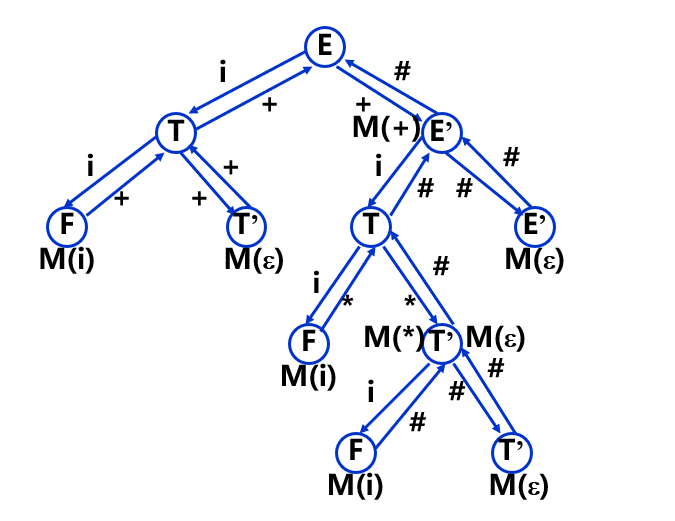
扩充的 BNF

BNF: 巴克斯摩尔范式.

扩充的 BNF: 在原有元语言符号 $\to, <, >, \mid$ 的基础上增加新的元语言符号, 使 BNF 的表达更为方便, 称为扩充的 BNF; 新引入的符号有:

$\{ \alpha \}$ 表示 $\alpha$ 的 0 次到任意多次重复, 即 $\alpha^*$
$\{ \alpha \}_0^n$ 表示 $\alpha$ 的 0 到 n 次重复.
$[\alpha]$ 表示 $\alpha$ 可有可无, 即 $\{ \alpha \}_0^1$

标识符的定义用扩充 BNF 表示为:

\left\{ \begin{array}{l} I \to \{ L \mid D \} \\ L \to a \mid b \mid ... \mid z \\ D \to 0 \mid 1 \mid ... \mid 9 \\ \end{array} \right.

使用扩充 BNF 的主要目的在于便于理解文法, 使得编写编译程序更加简便.

本文中, 扩充 BNF 只用于写递归下降分析器.

扩充的 BNF 也可以用转换图来表示.

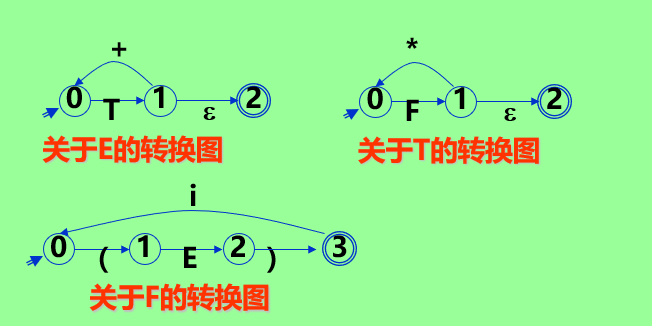
对上述文法 $G_1$ , 使用扩充 BNF 改写为:

\left\{ \begin{array}{l} E \to T \{ +T \} \\ T \to F \{ *F \} \\ F \to (E) \mid i \\ \end{array} \right.

根据扩充的 BNF 写出的递归下降分析器的代码:

func E() {
    T()
    for ;sym == '+'; advance() {
        T()
    }
}

func T() {
    F()
    for ;sym == '*'; advance() {
        F()
    }
}

func F() {
    if sym == 'i' {
        advance()
    } else if sym == '(' {
        advance()
        E()
        if sym == ')' {
            advance()
        } else {
            error()
        }
    } else {
        error()
    }
}

对串 $i+i*i$ 的分析如下:

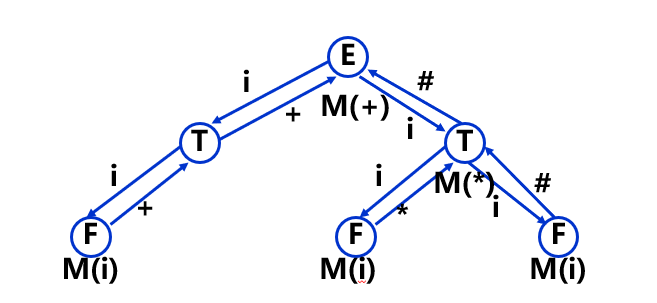
预测分析法

预测分析法: 预测分析(forecasting parse)是一种表驱动方法, 由下推栈/预测分析表和控制程序组成. 它是下推自动机(上下文无关文法的识别程序, 即: 下推自动机 == 上下文无关文法)的实现模型.

预测分析表

形式: $M[A, a]$ 是一张表, $A \in V_N$ 标记行, $a \in V_T \cup \{ \# \}$ 标记列.
表格单元内容: $A \to a$ 或出错标志(空白)

预测分析器的执行算法

预测分析程序总是按照栈顶符号 $X$ 和当前输入符号 $a$ 行事. 分析开始时, 栈底先放入一个 $\#$ , 然后放入文法的开始符号. 对任何 $(X, a)$ , 总控程序执行下述动作之一:

若 $X = a = '\#'$ , 分析成功, 且分析过程终止.
若 $X = a \ne '\#'$ , 把 $X$ 从栈顶上托, 并让 $a$ 指向下一个输入符号.
若 $X$ 是非终止符, 则查看分析表 $M$ , 若 $M[X, a]$ 中存放着 $X$ 的一个产生式, 则上托 $X$ , 并把产生式右部符号按照逆序推进栈; 若 $M[X, a]$ 是出错标志, 则调用出错处理程序 error().

$\#$ 为内容结束符, 由编译器为每段代码在结束处添加.

预测分析器和递归调用分析器的区别:

虽然两者都是自上而下的分析方法, 但是预测分析器的主控程序始终是不变的, 只需要为不同的文法生成不同的分析表, 也不用考虑回溯之类的问题.

例: 对于文法 $G_1'$ :

\left\{ \begin{array}{l} E \to TE' \\ E' \to +TE' \mid \epsilon \\ T \to FT' \\ T' \to *FT' \mid \epsilon \\ F \to (E) \mid i \end{array} \right.

有如下预测分析表:

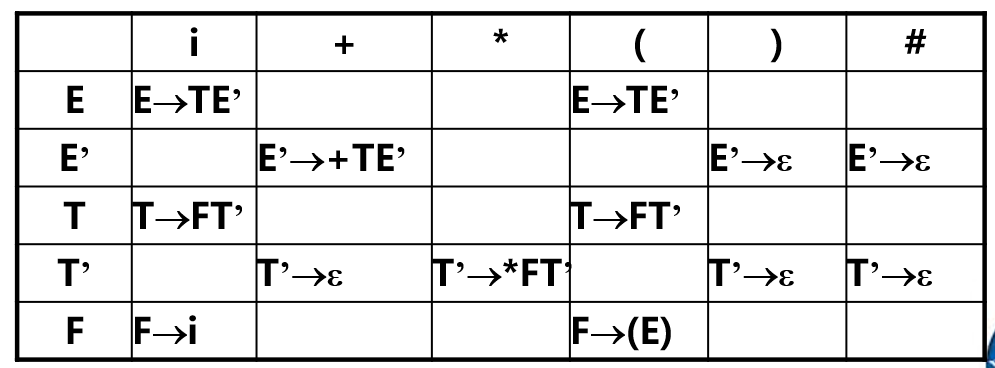
对于输入串 $i+i*i$ 使用预测分析法进行处理:

预测分析表的构造--集合

FIRST 集:

对 $\alpha \in (V_T \cup V_N)^*$ , 有:

$FIRST(\alpha) = \{ a \mid \alpha \Rightarrow a..., a \in V_T \}$ ,

若 $\alpha \Rightarrow \epsilon$ , 则 $\epsilon \in FIRST(\alpha)$

$FIRST(\alpha)$ 表示 $\alpha$ 可能推导出的所有首终结符或 $\epsilon$ 的集合.

FOLLOW 集:

对 $A \in V_N$ , 有:

$FOLLOW(A) = \{a \mid S \Rightarrow ...Aa... , a \in V_T$

若 $S \Rightarrow ...A$ , 则 $\# \in FOLLOW(A)$ , 其中 $S$ 为开始符号.

$FOLLOW(A)$ 表示所有句型中紧跟在 $A$ 后面出现的终结符的集合.

FIRST 集的构造方法:

对每个文法符号 $X \in V_T \cup V_N$ , 连续使用如下规则, 直到每个 $FIRST(X)$ 不再增大.

$X \in V_T$ , 则 $FIRST(X) = X$ ;
$X \in V_N$ , 且有 $X \to a..., a \in V_T$ , 则把 $a$ 加入 $FIRST(X)$ ; 若 $X \to \epsilon$ 也是产生式, 则把 $\epsilon$ 也加入 $FIRST(X)$ 中;
$X \to Y..., Y \in V_N$ , 则把 $FIRST(Y) - \{\epsilon\}$ 加入 $FIRST(X)$ ;
$X \to Y_1Y_2...Y_K$ , 且 $Y_1, Y_2, ..., Y_K \in V_N$ , $Y_1...Y_{i-1} \Rightarrow \epsilon$ , 则把所有 $FIRST(Y_j) - \{\epsilon\}$ 加入 $FIRST(X)$ , 其中 $1 \le j \le i$ ; 若 $Y_1...Y_K \Rightarrow \epsilon$ , 则把 $\{\epsilon\}$ 加入 $FIRST(X)$ .

对文法 $G$ 的任何符号串 $\alpha = X_1X_2...X_n$ 构造 $FIRST(\alpha)$ 的方法为:

首先把 $FIRST(X_1) - \{\epsilon\}$ 加入 $FIRST(\alpha)$ ;
若对任意 $1 \le j \le i - 1, \epsilon \in FIRST(X_j)$ , 则把 $FIRST(X_i)$ 加入 $FIRST(\alpha)$ 中;
如果所有 $FIRST(X_j)$ 都包含 $\epsilon$ , 则把 $\epsilon$ 加入 $FIRST(\alpha)$ 中.

FOLLOW 集的构造方法:

对每个文法符号 $A$ , 连续使用如下规则, 直到每个 $FOLLOW(A)$ 不再增大.

对于文法的开始符号, 把 $\#$ 加入 $FOLLOW(S)$ ;
对于产生式 $A \to \alpha B \beta$ , 把 $FIRST(\beta) - \{\epsilon\}$ 加入 $FOLLOW(B)$ ;
对于产生式 $A \to \alpha B$ 或者 $A \to \alpha B \beta, \beta \Rightarrow \epsilon$ , 将 $FOLLOW(A)$ 加入 $FOLLOW(B)$ .

FOLLOW 集中永远不会出现 $\epsilon$ .

预测分析表的构造--算法

设有文法 $G$ , 构造 $FIRST(\alpha)$ 和 $FOLLOW(A)$ , 然后执行如下算法:

对文法 $G$ 的每个产生式执行 (2), (3);
对每个 $a \in FIRST(\alpha)$ , 把 $A \to \alpha$ 放入 M[A, a];
若 $\epsilon \in FIRST(\alpha)$ , 则对所有 $b \in FOLLOW(A)$ , 把 $A \to \alpha$ 放入 M[A, b];
把所有无定义(空白)的 M[A, a] 标上"出错"标志.

注意:
上述算法可以对任何文法 $G$ 构造预测分析表. 有些文法的预测分析表可能有多重入口.
如果文法 $G$ 的预测分析表没有多重入口, 则称 $G$ 是 LL(1) 文法; 反之, $G$ 不是 LL(1) 文法.

预测分析表的具体实现

只将产生式 $A \to \alpha$ 的右部符号 $\alpha$ 填入 M[A, b] 中.
若 $\alpha = x_1x_2..x_n$ , 则将 $\alpha$ 的逆序 $x_nx_{n-1}...x_1$ 填入 M[A, b] 中.
若 $x_nx_{n-1}...x_1$ 中的 $x_1$ 是终结符, 则无需进栈, 直接将输入串指针指向下一个输入符.
为节省空间, 分析表可以只存储产生式标号, 产生式存储在其他地方.

自下而上的语法分析

引言--自下而上的语法分析

自下而上分析法: 从输入串出发, 寻找一个规约序列, 逐步向上规约, 直到文法的开始符号.

自下而上分析法的实现: 采用一个寄存文法符号的栈, 把输入符号逐个移进栈, 检查栈顶字符串是否形成某个产生式的一个候选式, 如果是, 就将其规约(替换)成该产生式的左部符号. 不断移进-规约, 直到栈中只剩下文法的开始符号.

对文法:

\left\{ \begin{array}{l} S \to SAS \\ S \to b \\ A \to ccA \\ A \to a \end{array} \right.

对输入串 $bccab$ 的规约过程如下:

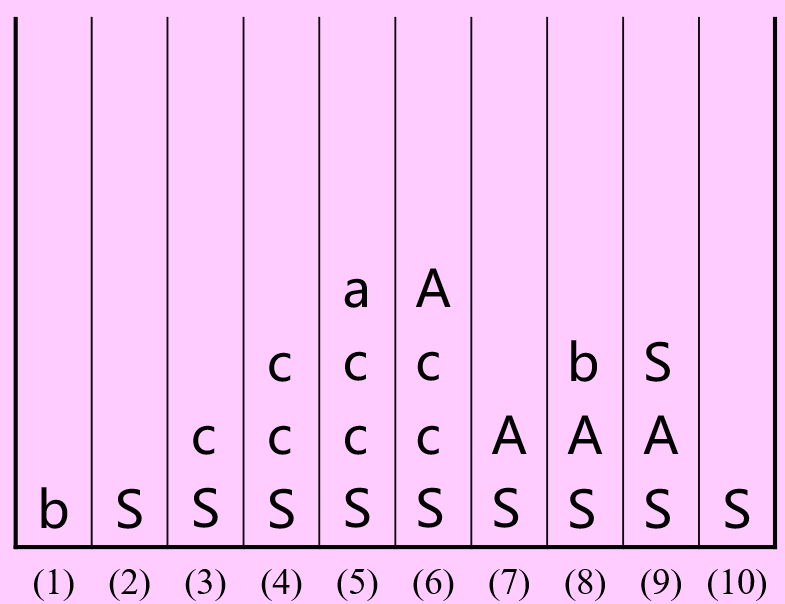
核心概念

短语

设有文法 $G$ , $S$ 是开始符号, 设 $\alpha\beta\gamma$ 是 $G$ 的一个句型, 若有:

S \Rightarrow \alpha A \gamma \\ A \Rightarrow \beta

则称 $\beta$ 是句型 $\alpha\beta\gamma$ 关于 $A$ 的短语.

直接短语

在上面定义中, 如果 $A$ 直接推出 $\beta$ , 则称 $\beta$ 是句型 $\alpha\beta\gamma$ 关于 $A \to \beta$ 的直接短语.

句柄

一个句型的最左直接短语称为句柄.

素短语

文法 $G$ 中某句型的一个短语 $\alpha$ 是素短语, 当且仅当它至少含有一个终结符, 且除它自身之外不在含有更小的素短语. 即: 素短语是包含终结符的最小短语.

最左素短语

在具有多个素短语的句型中处于最左边的那个素短语.

利用推导树进行判断

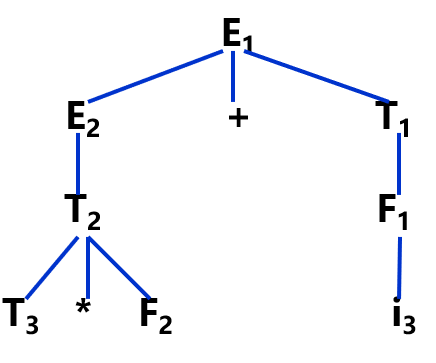
任何子树的边缘是子树根节点的短语.
只有一代的子树, 子树的边缘是子树根节点的直接短语.
推导树的最左直接短语即句柄.

算符优先分析法

一种直观, 简单, 有效的方法, 适合于表达式的分析. 但是不严格按照最左规约进行, 不是规范规约.

算符文法

如果一个文法的任何产生式都不含两个或者两个以上的相连的非终结符(即: 文法不包含 $P \to \epsilon$ 或 $P \to ...AB...$ ), 且不含 $\epsilon$ 产生式, 则称该文法为算符文法.

算符之间的优先关系

对算符文法 $G, \ a,b \in V_T, \ P,Q,R \in V_N$ , 定义:

$a = b$ : $G$ 中有 $P \to ...ab...$ 或 $P \to ...aQb...$ .
$a < b$ : $G$ 中有 $P \to ...aQ...$ 且 $Q \Rightarrow b...$ 或 $Q \Rightarrow Rb...$ .
$a > b$ : $G$ 中有 $P \to ...Qb...$ 且 $Q \Rightarrow ...a$ 或 $Q \Rightarrow ...aR$

算符优先文法

如果算符文法 $G$ 的任何两个终结符之间的关系最多只有 $<,=,>$ 中的一个优先关系, 则称该文法为算符优先文法.

优先关系表

用一个表格记录一个文法 $G$ 中的所有终结符之间的优先关系, 称为优先关系表.

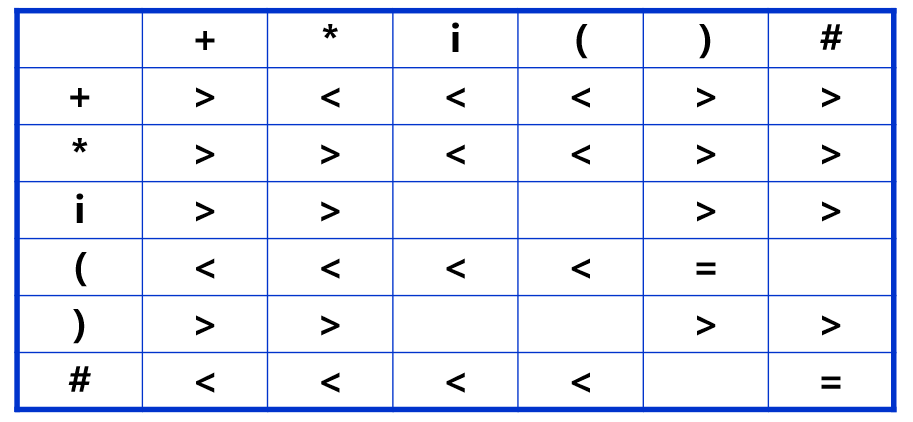
注意:
优先关系不是数学关系,
$a < b$ , 未必有 $b > a$ .
终结符之间未必有优先关系.
优先关系不能传递.

算符优先文法 $G$ 的任何句型的最左素短语是满足如下条件的最左串 $N_j a_j N_{j+1} ...N_i a_i N_{i+1}$ , 其中:

$a_{j-1} < a_j$
$a_j = a_{j+1},...,a_{i-1} = a_i$
$a_i > a_{i+1}$

算符优先分析法的实现

使用一个分析栈, 当栈顶形成最左素短语时, 进行规约.

对于文法 $G_1$ :

\left\{ \begin{array}{l} E \to T \mid E + T \\ T \to F \mid T*F \\ F \to (E) \mid i \\ \end{array} \right.

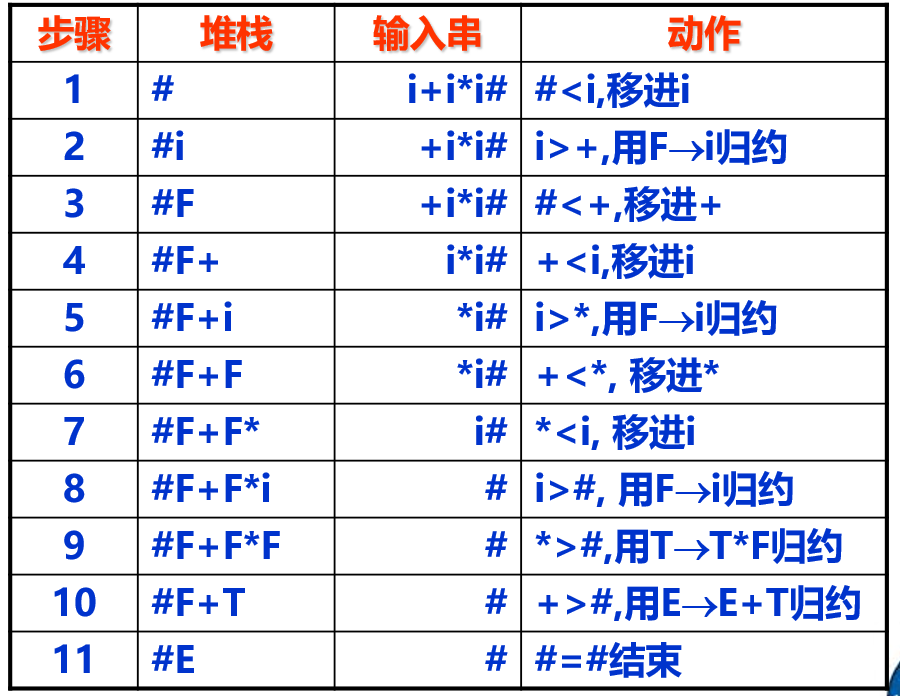
规约的操作流程:

设栈顶终结符为 $a$ (如果栈顶符号是终结符, 则 $a$ 对应该终结符; 若栈顶符号是非终结符, 则 $a$ 对应次栈顶符号); 设 $b$ 是当前输入字符; M[a, b] 是文法的优先关系表.

初始化: $\#$ 入栈; 输入出啊末尾添加 $\#$ ; 输入指针指向第一个输入符号.
M[a, b] 为 $<$ 或 $=$ 时,移进 $b$ , 输入指针指向下一个输入字符.
M[a, b] 为 $>$ 时, 将栈顶包含 $a$ 的素短语按照相应的产生式进行规约.
M[a. b] 为空白时, 出错处理.
$A = B = \#$ , 分析成功.

优先关系表的构造

FIRSTVT 集: $FIRSTVT(P) = \{a \mid P \Rightarrow a...\ Or P \Rightarrow Qa..., \ a \in V_T, Q \in V_N\}$
非终结符 $P$ 能推出的第一个终结符的集合.
LASTVT 集: $LASTVT(P) = \{a \mid P \Rightarrow ...a\ Or P \Rightarrow aQ..., \ a \in V_T, Q \in V_N\}$
非终结符 $P$ 能推出的最后一个终结符的集合.

构造算法如下:

FIRSTVT 集: 对文法连续使用下面规则求 $FIRSTVT(P)$ $F I RST V T (P)$ , 直到其不再增大.
1. 如果有产生式 $P \to a...$ 或 $P \to Qa...$ , 则 $a \in FIRSTVT(P)$ .
2. 如果有产生式 $P \to Q...$ , 则 $FIRSTVT(Q) \subseteq FIRSTVT(P)$ .
LASTVT 集: 对文法连续使用下面规则求 $LASTVT(P)$ $L A ST V T (P)$ , 直到其不再增大.
1. 如果有产生式 $P \to ...a$ 或 $P \to ...Qa$ , 则 $a \in LASTVT(P)$ .
2. 如果有产生式 $P \to ...Q$ , 则 $LASTVT(Q) \subseteq LASTVT(P)$ .

矩阵构造算法:

P 为非终结符, a 为终结符.

FIRSTVT 集:
1. 如果有产生式 $P \to a...$ 或 $P \to Qa...$ , 则 M[P, a] = 1.
2. 如果有产生式 $P \to Q...$ , 则对所有 M[Q, a] = 1, 令 M[P, a] = 1.
3. 重复直至 M 不再扩大.
LASTVT 集:
1. 如果有产生式 $P \to ...a$ 或 $P \to ...Qa$ , 则 M[P, a] = 1.
2. 如果有产生式 $P \to ...Q$ , 则对所有 M[Q, a] = 1, 令 M[P, a] = 1.
3. 重复直至 M 不再扩大.

LR 分析法

LR 分析法是一种自下而上的分析方法, 其功能强大, 适用于一大类文法. 它在从左向右扫描输入串的同时, 能及时发现输入串的错误, 并能准确指出错误的位置. LR 的意思是: 自左向右扫描, 自下而上规约.

LR 分析器实现: LR 分析器主要由两部分组成:

总控程序: 对于所有文法都是一样的, 易于实现.
分析表: 不同的文法分析表不同.

LR 分析法的种类:

LR(0)
SLR
LR(1)
LALR
LR(k)

LR 分析过程

LR 分析法是一种表驱动分析法, 由一个分析栈, 控制程序和分析表及输入串组成, 如下图:

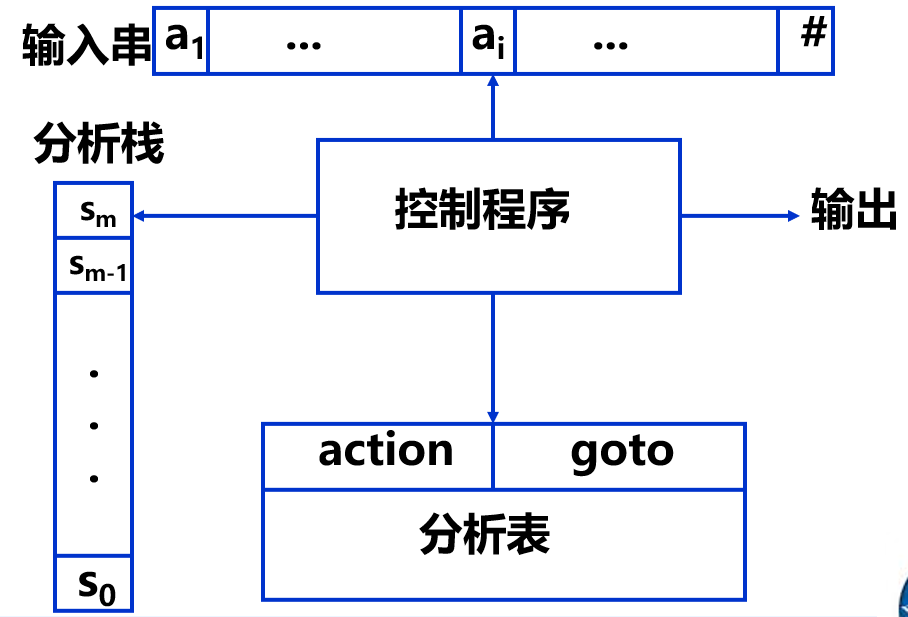
action 表

action 表是一个状态及终结符的二维矩阵, action 定义了在状态 s 下, 当输入字符为 a 时, 分析器应采取分析动作:

action[s, a] = shift j, 将状态 j 以及当前输入字符移进分析栈栈顶, 简记为 $s_j$ .
action[s, a] = reduce j, 将栈顶内容按第 j 个产生式规约, 简记为 $r_j$ .
action[s, a] = accept, 分析成功, 输入串被接受, 简记为 $acc$ .
action[s, a] = error, 语法错误, 简记为空白.

goto 表

goto 表是一个状态及非终结符的二维矩阵, goto[s, X] 定义了在状态 s 下, 面对文法符号 X 时的状态转换.

控制程序

控制程序执行如下动作:

初始化: 分析栈分为状态栈和符号栈. 初始化时, 状态栈置状态 $0$ , 符号栈放入 $\#$ ; 根据状态栈顶状态 $s$ , 以及当前输入符号 $a$ , 执行如下操作:
如果 action[s, a] = shift j, 将状态 $j$ 以及当前输入字符移进分析栈栈顶, 输入指针指向下一个输入字符.
如果 action[s, a] = reduce j, 则按照第 $j$ 个产生式 $A \to \alpha$ 规约, 设 $\mid \alpha \mid = t$ , 则将分析栈顶 $t$ 个符号移出栈, 再根据当前栈顶状态 $s$ , 以及规约后的非终结符 $A$ , 查 goto 表. 如果 goto[s, A] = k, 则将状态 $k$ 以及非终结符 $A$ 移进栈.
如果 action[s, a] = accept, 分析成功, 输入串被接受.
如果 action[s, a] 或者 goto[s, A] 为 error, 转到错误处理程序.

对于文法 $G_1$ :

\left\{ \begin{array}{l} E \to T \mid E + T \\ T \to F \mid T*F \\ F \to (E) \mid i \\ \end{array} \right.

分析表如图:

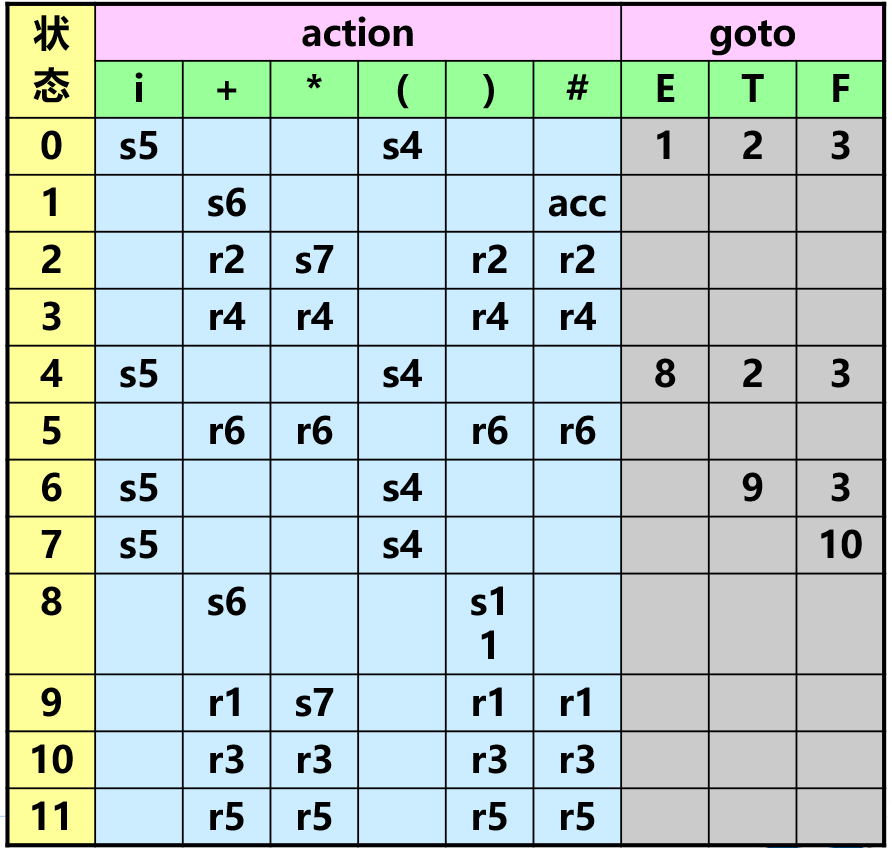
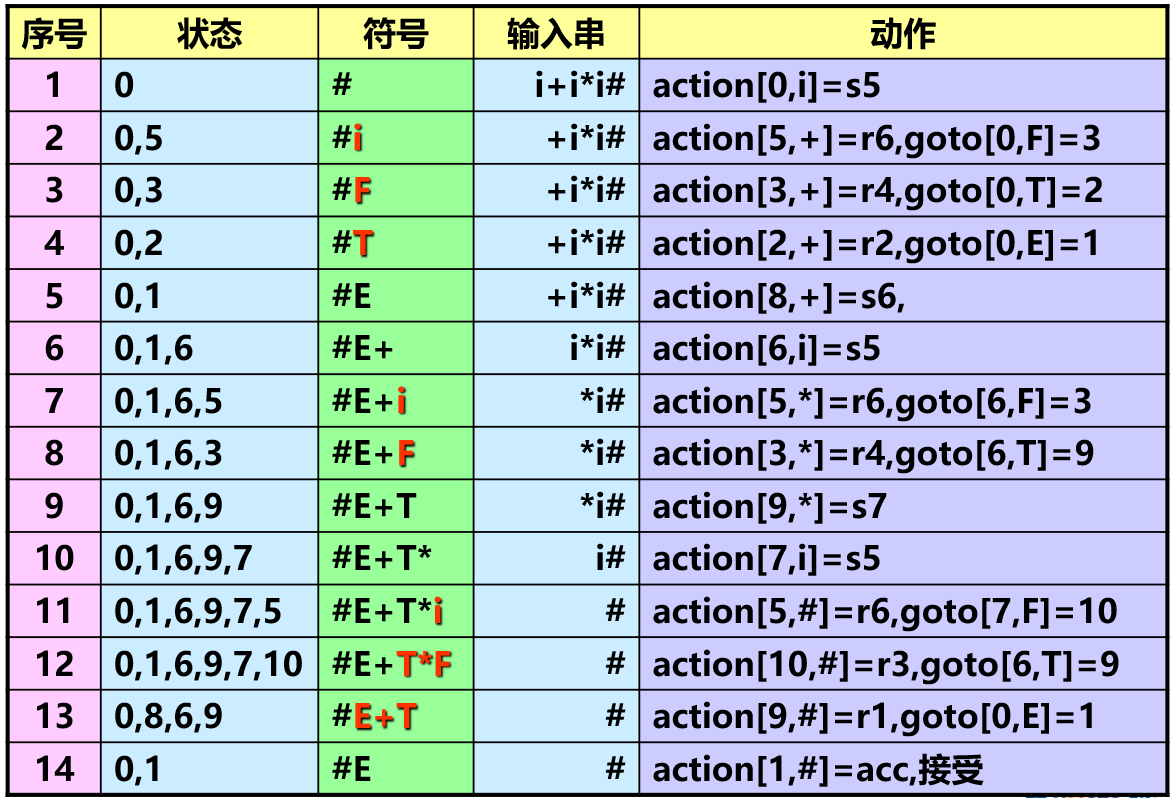
LR 分析的特点

规约符号串总是在栈顶.
句柄之后的待入栈符号串总是终结符.
规范句型(由规范推导推出的句型)在符号栈中的符号串总是规范句型的前缀.

活前缀

规范句型中不含句柄之后任何符号的一个前缀, 称为该规范句型的活前缀. 即: 若 $A \to \alpha\beta$ 是文法的一个产生式, $S$ 为文法的开始符号, 并有: $S \Rightarrow \gamma A\omega \Rightarrow \gamma\alpha\beta\omega$ , 则 $\gamma\alpha\beta$ 的任何前缀都是 $\gamma\alpha\beta\omega$ 的活前缀.

上述定义表明 $\alpha\beta$ 是规范句型的句柄.

活前缀和句柄之间可能有如下关系:

活前缀不含句柄的任何符号: 期望从后续输入串中识别由 $A \to \alpha\beta$ 中的 $\alpha\beta$ 产生的字符串.
活前缀只含有句柄的真前缀: 产生式 $A \to \alpha\beta$ 中的 $\alpha$ 已经被识别出在分析栈的栈顶上, 期待从剩余输入串中识别由 $\beta$ 所能推导的符号串.
活前缀已经包含句柄的全部符号: 产生式 $A \to \alpha\beta$ 的右部符号 $\alpha\beta$ 已经在分析栈的栈顶, 应将其规约为 $A$ .

结论:

句柄是活前缀的后缀, 如果能识别一个文法的所有活前缀, 就能识别这个文法的所有句柄.

活前缀的识别

LR-0 项目

在一个产生式右部添加一个原点, 称为一个 LR(0) 项目.

其中, 句柄和活前缀的关系为:

$A \to \cdot \alpha\beta$ : 活前缀不包含句柄的任何字符.
$A \to \alpha\cdot\beta$ : 活前缀包含句柄的真前缀.
$A \to \alpha\beta$ : 活前缀包含句柄的所有字符.

LR(0) 项目中的 $\cdot$ , 表示识别的位置. $\cdot$ 左边是已识别部分, 右边是期待识别的部分.

LR(0) 项目的分类:

规约项目: 形如: $A \to \alpha\cdot$ .
移进项目: 形如: $A \to \alpha\cdot a\beta, \ a \in V_T$ . (遇到终结符, 继续移进).
待约项目: 形如: $A \to \alpha\cdot B \beta, \ B \in V_N$ . (遇到非终结符, 准备规约).
接受项目: 形如: $S \to \alpha\cdot$ , $S$ 为开始符号.

文法的拓广:

在文法 $G$ 中增加产生式 $S' \to S$ , 从而使 $S' \to S\cdot$ 成为唯一的接受项目, 称为文法的拓广.

构造识别所有活前缀的转换图:

每个状态是一个 LR(0) 项目.
$S' \to \cdot S$ 是唯一的初态.
所有的其他项目是终态, 是某个活前缀的识别态.
若状态 $i$ 为 $X \to X_1 ... X_{i-1}\cdot X_i...X_n$ , 状态 $j$ 为 $X \to X_1 ... X_i\cdot X_{i+1}...X_n$ , 则从状态 $i$ 画一条有向边到状态 $j$ , 标记为 $X_i$ .
如果 $X_i$ 为一个非终结符, 并有 $X_i \to \alpha_1 \mid \alpha_2 \mid ... \mid \alpha_m$ , 则从状态 $i$ 画 $\epsilon$ 有向边到所有状态 $X_i \to \cdot \alpha_i$ .

上面的算法构造的是一个识别所有活前缀的非确定有限自动机.

对于文法 $G_2$ 拓广后的 $G_2'$ :

\left\{ \begin{array}{l} S' \to S \\ S \to BB \\ B \to aB \\ B \to b \\ \end{array} \right.

文法 $G_2'$ 的所有 LR(0) 项目为:

\left\{ \begin{array}{l} S' \to \cdot S \\ S' \to S \cdot \\ S \to \cdot BB \\ S \to B \cdot B \\ S \to BB \cdot \\ B \to \cdot aB \\ B \to a \cdot B \\ B \to aB \cdot \\ B \to \cdot B \\ B \to b \cdot \\ \end{array} \right.

其活前缀的状态转换图为:

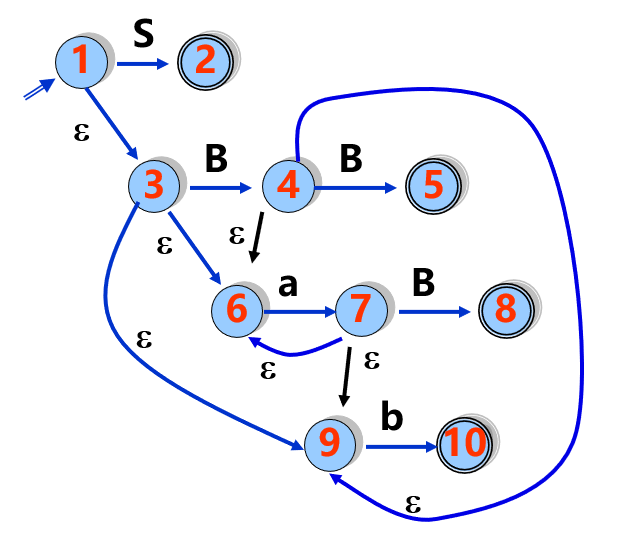
StateTransitionDiagramForLR0ProjectOfG2Plus

其中, 双圈代表句柄别态.

构造识别文法所有活前缀的确定自动机

有效项目: 对于项目 $A \to \alpha \cdot \beta$ , 如果有 $S \Rightarrow \gamma A \omega \Rightarrow \gamma\alpha\beta\omega$ , 则称项目 $A \to \alpha \cdot \beta$ 对活前缀 $\gamma\alpha$ 有效.

有效项目集: 对于一个活前缀有效的项目可能不止一个, 对活前缀 $\gamma\alpha$ 有效项目集.

LR(0) 项目集规范族: 文法 $G$ 的所有有效项目集组成的称为文法 $G$ 的 LR(0) 项目集规范族.

LR(0) 项目集规范族的构造:

$closure(I)$ $c l os u re (I)$ : 设 $I$ $I$ 是一个 LR(0) 项目集, $closure(I)$ $c l os u re (I)$ 按如下规则构造:
- 对任何 $i \in I$ , 都有 $i \in closure(I)$
- 若项目 $A \to \alpha \cdot B \beta \in closure(I)$ , 且 $B \to \omega$ 是文法的一个产生式, 则 $B \to \cdot \omega \in closure(I)$
- 重复直到 $closure(I)$ 不再增大
$go(I, X)$ : 设 $I$ 是一个 LR(0) 项目集, $X$ 是文法符号, 状态转换函数 $go(I, X)$ 定义为:
$go(I, X) = closure(\{A \to \alpha X \cdot\beta \mid A \to \alpha \cdot X \beta \in I\})$

对于上面的 (2), 即: 如果项目 $A \to \alpha \cdot X \beta$ 对 $\gamma \alpha$ 有效, 则 $A \to \alpha X \cdot \beta$ 对 $\gamma \alpha X$ 有效. 即: 如果 $I$ 是对 $\gamma \beta$ 有效的项目集, 则 $go(I, X)$ 是对 $\gamma \beta X$ 有效的项目集.

算法如下:

begin
  C := closure({S' -> .S}); // C := closure(StartCondition)
  repeat
    for (C 中的每个项目集 I 和 文法符号 X) do
      if (go(I, X) != null && go(I, X) not in C)
      then 将 go(I, X) 加入 C;

      <!--
      if (go(I, X) in C)
      then 将 go(I, X) = I' 加入到 goto 表
      -->
  until C 不再增大;
end

LR-0 分析表的构造

如果 $A \to \alpha \cdot a \beta \in I_k$ , 且 $go(I_k, a) = I_j, \ a \in V_T$ , 则 $action[k, a] = s_j$ .
如果 $A \to \alpha \cdot \in I_k$ , $A \to \alpha$ 为第 $j$ 个产生式, 则对所有终结符 $b$ 或者 $\#$ , $action[k, b] = r_j$ .
如果 $S' \to S \cdot \in I_k$ , 则 $action[k, \#] = acc$ .
如果 $go(I_k, A) = I_j, \ A \in V_N$ , 则 $goto[k, A] = j$ .
凡是不能用以上规则登记的表项均为错误.

对于文法 $G_2'$ , LR(0) 分析表如下:

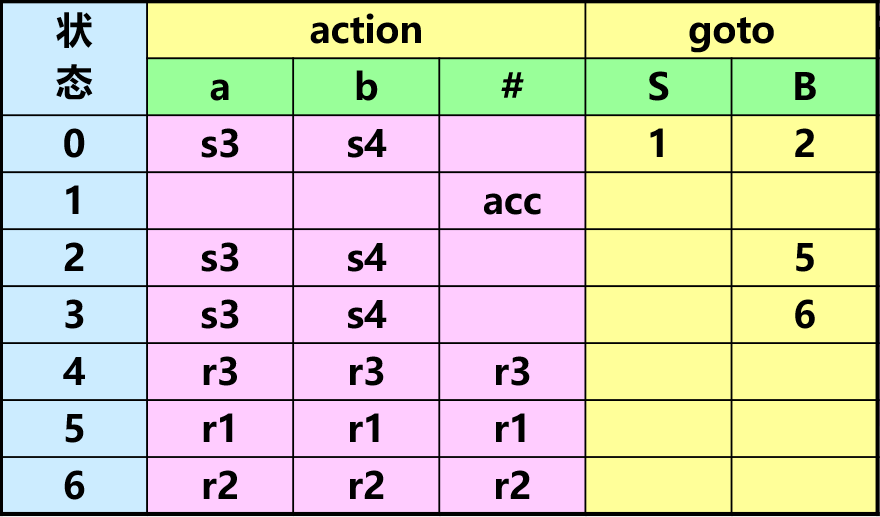
如果一个文法的 LR(0) 项目集规范族的项目中, 既包含移进项目, 又包含规约项目, 称为移进-规约冲突. 如:

对于文法 $G_1$ 拓广后的文法 $G_1'$ :

\left\{ \begin{array}{l} S' \to \cdot S \\ E \to E + T \\ E \to T \\ T \to T * F \\ T \to F \\ F \to (E) \\ F \to i \\ \end{array} \right.

得到的 LR(0) 项目集规范族:

...\\ I_9 = \{E \to E + T \cdot, T \to T \cdot * F\} \\ ...

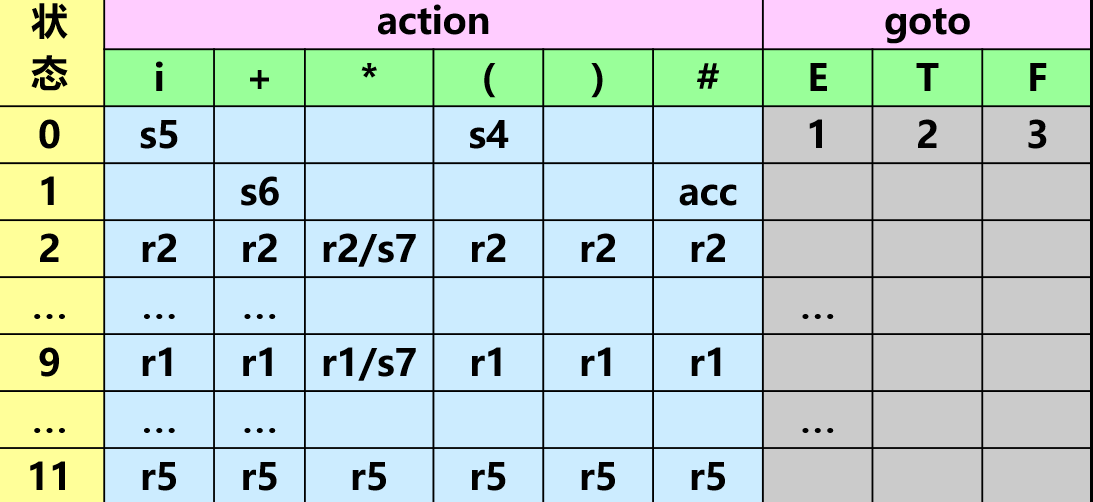
此时, 分析表对应项中存在多重入口.

注意:
如果文法 $G$ 的 LR(0) 分析表没有多重入口, 则称 $G$ 为 LR(0) 文法.

SLR-1 分析表构造

通过考察有关非终结符的 $FOLLOW$ 集来解决移进-规约和规约-规约冲突, 以此构造出来的 LR 分析表, 称为 SLR(1) 分析表.

如: 假定一个 LR(0) 项目集规范族有一个项目集 I:

I = \{X \to \alpha \cdot b \beta, A \to \alpha \cdot, B \to \alpha \cdot\}

当状态 I 面临任何输入符号 $\alpha$ 时, 可以采用如下策略:

如果 $\alpha = b$ , 移进.
如果 $\alpha \in FOLLOW(A)$ , 用产生式 $A \to \alpha$ 规约.
如果 $\alpha \in FOLLOW(B)$ , 用产生式 $B \to \alpha$ 规约.
此外, 报错.

如果文法 $G$ 的 SLR(1) 分析表没有多重入口, 则称 $G$ 为 SLR(1) 文法. 并非所有的文法都是 SLR(1) 文法.

语义分析和中间代码生成

语义分析概述

语义分析的任务:

语义检查: 主要进行一致性检查和越界检查.
语义处理:
- 说明语句: 通常将其中定义的名字及属性信息记录在符号表中, 以便进行存储分配.
- 执行语句: 生成语义上等价的中间代码, 实现将源程序翻译成中间代码的过程.

一致性检查: 表达式中操作数是否保持类型一致? 赋值语句左右两边是否类型一致? 形参-实参类型是否一致? 数组元素与数组说明是否一致? ...
越界检查: 数组下标是否越界? 子界类型是否越界?

语法制导翻译: 在语法分析过程中, 根据每个产生式对应的语义子程序(语义动作)进行翻译(生成中间代码)的方法.

语义子程序: 完成语义检查和予以处理后, 每个产生式对应一个语义子程序, 每当使用这个产生式进行规约或者匹配时, 调用相应的语义子程序进行翻译.

语义值: 在描述语义动作时, 需要赋予每个文法符号以各种不同的值, 这些值统称为语义值. 例如: 类型, 种属, 地址或代码等, 通常使用 X.TYPE, X.CAT, X.VAL 来表示这些值.

例: 对于文法:

\left\{ \begin{array}{l} E \to E + E \\ E \to 0 \\ E \to 1 \\ \end{array} \right.

可以写出如下语义子程序:

\left\{ \begin{array}{l} E \to E_1 + E_2 \ \{E.VAL := E_1.VAL + E_2.VAL\} \\ E \to 0 \ \{E.VAL := 0\} \\ E \to 1 \ \{E.VAL := 1\} \\ \end{array} \right.

中间代码

中间代码是一种与机器无关的抽象代码, 有多种形式:

逆波兰表示(后缀式)
三地址代码
树
间接三元式
四元式
...

三地址代码是一种普遍采用的中间代码表示, 形式如下:

x = y op z

常用的三地址语句有:

二元运算赋值语句: x = y op z
一元运算赋值语句: x = op z
复写类赋值语句: x = y
变址类赋值语句: x = y[i], x[i] = y
地址和指针类赋值语句: x = &y, x = *y, *x = y
无条件转移语句: goto L
条件转移语句: if x rop y goto L, if a goto L
过程调用和参数传递语句:
```
param x1
param x2
...
call P, n
```
过程返回语句: return y

例如: 赋值语句 a := -b * c + d 可以翻译如下三地址语句:

t1 = uminus b
t2 = t1 * c
t3 = t2 + d
a = t3

语义变量和语义函数

i.NAME: 语义变量, 表示与 i 相关普通变量的标识符字符串.
E.PLACE: 语义变量, 表示存放 E 值的变量名在符号表中的位置(普通变量)或整数编码(临时变量).
newtemp(): 语义函数, 每调用一次, 产生一个新的临时变量.
entry(i): 语义函数, 对变量 i 查符号表, 如果 i 在符号表中, 则返回它在符号表中的位置; 如果不在, 返回 0.
emit(RESULT, OPD1, oper, OPD2) 或 emit(RESULT, oper, OPD): 语义函数, 根据参数产生三地址语句, 并放到 ip 指针指向的位置, ip 指针加 1.
error(): 语义函数, 错误处理.

说明语句的翻译

说明语句有很多种, 这里只讨论变量的类型说明.

变量的类型说明一般具有如下的文法形式:

<类型说明> \to <变量名表>:<类型> \\ <变量名表> \to <变量名表>,<变量> \mid <变量> \\

说明语句的翻译主要是将说明信息存入到相应的描述符中.

变量的主要信息有:

变量名(NAME)
变量的类型(TYPE)
变量在局部区域的相对地址(OFFSET)

考虑一个简单的变量类型说明:

\left\{ \begin{array}{l} D \to i:T \mid D; D \\ T \to real \mid integer \mid array[num] \; of \; T_1 \mid *T \\ \end{array} \right.

类型定义为:

real: 实型
integer: 整形
array[num] of T1: 类型为 T1 类型的数组
*T: 指针类型

为变量初始化增加开始符和终结符, 增加产生式:

\left\{ \begin{array}{l} S \to MD \\ M \to \epsilon \\ \end{array} \right.

说明语句的语义子程序如下:

$M \to \epsilon$

{
  OFFSET := 0
}

$D \to i:T$

{
  enter(i.NAME, T.TYPE, OFFSET);
  OFFSET := OFFSET + T.WIDTH;
}

$T \to integer$

{
  T.TYPE := integer;
  T.WIDTH = 2;
}

$T \to real$

{
  T.TYPE := real;
  T.WIDTH := 4;
}

$T \to array[num] \ of \ T_1$

{
  T.TYPE := array(num.val, T1.TYPE);
  T.WIDTH := num.val * T1.WIDTH;
}

$T \to *T_1$

{
  T.TYPE := pointer(T1.TYPE);
  T.WIDTH := 4;
}

$D \to D;D$

{}

$S \to MD$

{}

赋值语句的翻译

为了简化问题, 只讨论简单变量的赋值语句的翻译, 不包括函数和数组元素. 假定使用自下而上的语法分析方法.

具有同一类型的赋值语句的翻译

假定表达式的文法为:

\left\{ \begin{array}{l} A \to i:=E \\ E \to E_1 \ OP \ E_2 \\ E \to i \\ E \to (E_1) \\ E \to -E_1 \\ \end{array} \right.

翻译后的语义子程序为:

$A \to i:=E$

{
  P := entry(i.NAME);
  if (P != 0) emit(P, =, E.PLACE);
  else error();
}

$E \to E_1 \ OP \ E_2$

{
  E.PLACE := newtemp();
  emit(E.PLACE, E1.PLACE, OP, E2.PLACE);
}

$E \to (E_1)$

{
  E.PLACE := E1.PLACE;
}

$E \to -E_1$

{
  E.PLACE := newtemp();
  emit(E.PLACE, uminus, E1.PLACE);
}

$E \to i$

{
  // 查符号表, 取得 i 的地址
  P := entry(i.NAME);
  // 如果 i 存在, 就把 E 指向 i 的地址
  if (P != 0) E.PLACE = P;
  else error();
}

注意: 子程序是没有考虑类型的.

例: 对于赋值语句 a := -b * c + d:

具有不同类型的赋值语句的翻译

变量具有整形和实型.
不同类型进行计算时, 整形向实型转化.

对于子程序 $E \to E_1 \ OP \ E_2$

{
  t := newtemp();
  E.TYPE := real;
  if (E1.TYPE = integer and E2.TYPE = integer) {
    emit(t, E1.PLACE, op_integer, E2.PLACE);
    E.TYPE := integer;
  } else if (E1.TYPE = real and E2.TYPE = real) {
    emit(t, E1.PLACE, op_read, E2.PLACE);
  } else if (E1.TYPE = integer and E2.TYPE = real) {
    t1 := newtemp();
    // itr: integer to real operator
    emit(t1, itr, E1.PLACE);
    emit(t, t1, op_real, E2.PLACE);
  } else {
    t1 := newtemp();
    emit(t1, itr, E2.PLACE);
    emit(t, t1, op_real, E1.PLACE);
  }
  E.PLACE := t;
}

控制语句的翻译

布尔表达式的翻译

假定具有如下文法:

B \to b \\ B \to i_1 \ rop \ i_2 \\

$b$ 为布尔变量, $rop$ 为关系运算符.

假定布尔表达式用于控制语句, B.T 表示布尔表达式为真时, 控制转移到的三地址语句的位置; B.F 表示布尔表达式为假时, 控制转移到的三地址语句的位置.

在生成该语句时, B.T 为: B 为真时条件转移语句本身的地址. B.F 为: B 为假时, 无条件转移语句本身的地址.

翻译后的语句子程序:

$B \to b$

{
  // ip 为下一条三地址语句的编号
  B.T := ip;
  emit(jnz, entry(b), 0);
  B.F := ip;
  emit(j, 0);
}

// 或者
{
  B.T := ip;
  B.F := ip + 1;
  emit(jnz, entry(b), 0);
  emit(j, 0);
}

$B \to i_1 \ rop \ i_2$

{
  B.T := ip;
  B.F := ip + 1;
  emit(jrop, entry(i1), entry(i2), 0);
  emit(j, 0);
}

无条件转移语句的翻译

假定无条件转移语句有如下文法:

\left\{ \begin{array}{l} label \to i: \\ S \to goto \ L \\ \end{array} \right.

goto L 有两种情况;

如果 L 已定义: 直接查表生成三元式.

如果 L 未定义:

将 L 记入符号表, 设置类型为标号(label), 定义否(IsDefined)标记位记为未(false), 地址域为当前 ip 序号.
在定义 L 处, 将 IsDefined 标记为 true. 把地址栏中的链首 r 取出, 执行 backpatch(r, ip) 回填标号 i 的引用链.

对于多个未定义符号引用, 将其设置为一条三地址语句的引用链, 链首记录在符号表中.

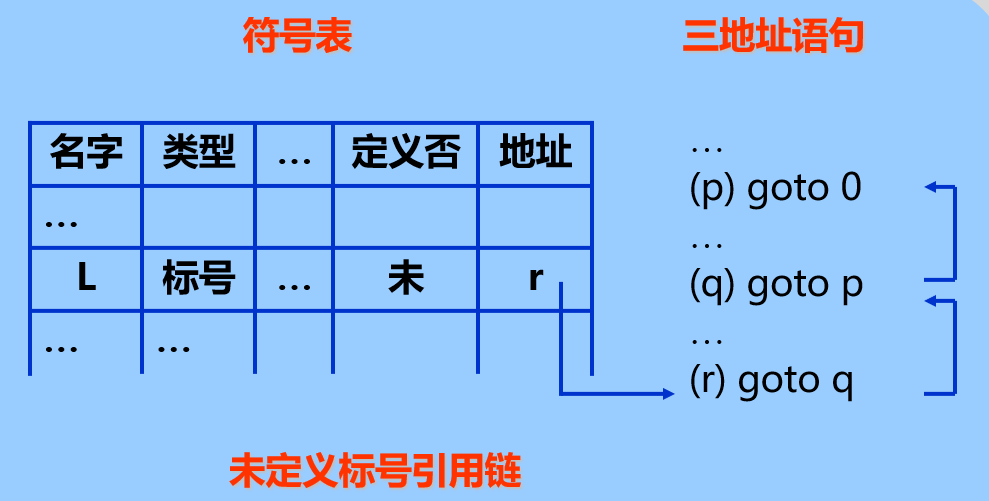
用 $label \to i:$ 规约时, 方式如下:

{
  // 对 i查 符号表
  P := entry(i.NAME);

  if (P = 0) {
    // 如果 i 不存在, 存入符号表, 设置为 已定义.
    enter(i.NAME, LABEL, OFFSET);
    i.IS_DEFINED := 1;
    i.ADDRESS := ip;
    OFFSET := OFFSET + LABEL.WIDTH;
  } else {
    // 如果 i 存在
    if (i.TYPE != LABEL) {
      // 但是类型不为 标号 LABEL, 报错
      error();
    } else if (i.IS_DEFINED = 0) {
      // i 存在, 但是没有定义, 设置为 已定义
      i.IS_DEFINED := 1;
      // 取出地址栏的链首 r
      ...
      // 回填标号 i 的引用链
      backpatch(r, ip);
    }
  }
}

用 $S \to goto \ L$ 规约时,

{
  // 对 L 查符号表
  P := entry(L.NAME);

  if (P = 0) {
    // 如果 L 不存在, 将 L 填入, 设置为 未定义, 生成三地址语句 goto 0
    enter(L.NAME, LABEL, OFFSET);
    L.IS_DEFINED := 0;
    emit(j, 0);
    OFFSET := OFFSET + LABEL.WIDTH;
  } else {
    if (L.TYPE = LABEL) {
    // 如果 L 存在
      if (L.IS_DEFINED = 1) {
        // 并且 L 已定义, 生成三地址语句 goto L
        emit(j, L.ADDRESS);
      } else {
        // L 未定义, 生成三地址语句 goto 0
        emit(j, 0);
        // 更新标号 L 的引用链
        ...
      }
    }
  }
}

条件语句的翻译

条件语句具有如下文法:

\left\{ \begin{array}{l} S \to if \ B \ then \ S_1 \\ S \to if \ B \ then \ S_1 \ else \ S_2 \\ \end{array} \right.

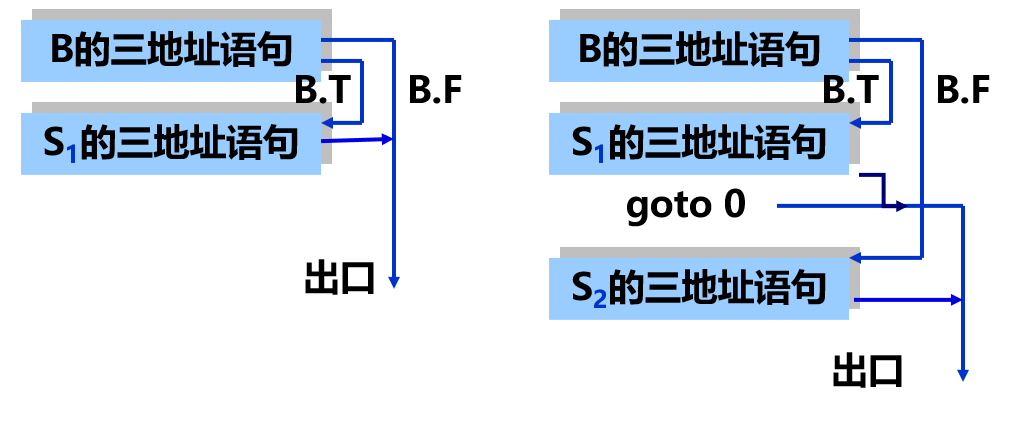
对于第一种:

生成 B 的三地址语句时, 一个 B.T 真出口, 一个 B.F 假出口. 生成它们时, 它们的转移地址均不知道.
生成 S1 的三地址语句时, 回填 B.T.
出口处转移地址未知, 等待回填, 形成回填链, 链首记录在 S.CHAIN.

对于第二种:

生成 B 的三地址语句时, 一个 B.T 真出口, 一个 B.F 假出口. 生成它们时, 它们的转移地址均不知道.
生成 S1 的三地址语句时, 回填 B.T. goto 0 为转出条件语句.
生成 S2 的三地址语句时, 回填 B.F.
出口转移地址未知, 等待回填, 形成回填链, 链首记录在 S.CHAIN.

条件语句 $if \ B \ then \ S_1$ 的语义子程序为(注意文法改写):

$M \to if \ B \ then$

{
  backpatch(B.T, ip);
  M.CHAIN := B.F;
}

$S \to MS_1$

{
  // merg(P1, P2) 为语义过程, 合并两条链, 并返回新的链首.
  S.CHAIN := merg(M.CHAIN, S1.CHAIN);
}

条件语句 $if \ B \ then \ S_1 \ else \ S_2$ 的语义子程序为:

$M \to if \ B \ then$

{
  backpatch(B.T, ip);
  M.CHAIN := B.F;
}

$N \to MS_1 \ else$

{
  q := ip;
  emit(j, 0);
  backpatch(M.CHAIN, ip);
  N.CHAIN := merg(S1.CHAIN, q);
}

$S \to NS_2$

{
  S.CHAIN := merg(N.CHAIN, S2.CHAIN);
}

例: 对于条件语句 if a < b then a := a + b else a := a - b:

注意: 如果语句 $S$ 后跟紧分号, 则 S.CHAIN 应回填 ip 的当前值, 可用下面的产生式及语义子程序来处理这种情况.

L \to S \mid L;S

语义子程序:

$L \to S$

{
  L.CHAIN := S.CHAIN.
}

$L \to XS$

{
  L.CHAIN := S.CHAIN;
}

$X \to L;$

{
  backpatch(L.CHAIN, ip);
}

while 语句的翻译

条件语句具有如下文法:

S \to while \ B \ do \ S_1

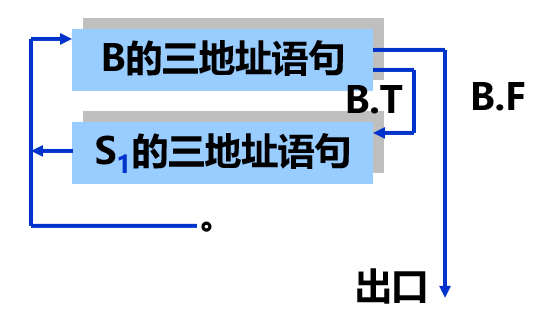
改写文法后的子程序为:

$W \to while$

{
  // 记录 B 的第一条三地址语句编号
  // CODE 记录的是一个控制语句基本块的入口地址, 一般为循环的首个条件语句地址.?
  W.CODE := ip;
}

$D \to W B \ do$

{
  // 回填真链
  backpatch(B.T, ip);
  D.CHAIN := B.F;
  D.CODE := W.CODE;
}

$S \to DS_1$

{
  // S 出口转向 B 的第一条语句
  backpatch(S1.CHAIN, D.CODE);
  // 产生无条件语句, 转向 B 的第一条语句
  emit(j, D.CODE);
  S.CHAIN := D.CHAIN;
}

例: 对于语句 while A > B do if U > V then E := F + G:

for 循环语句的翻译

文法: $S \to for \ i := E_1 \ step \ E_2 \ until \ E_3 \ do \ S_1$ .

假定步长表达式 $E_2$ 总为正值, 以上循环语句的语义为:

{
  i := E_1;
  goto over;
  again: i := i + E2;
  over: if (i <= E3) {
    S1'
    goto again;
  }
}

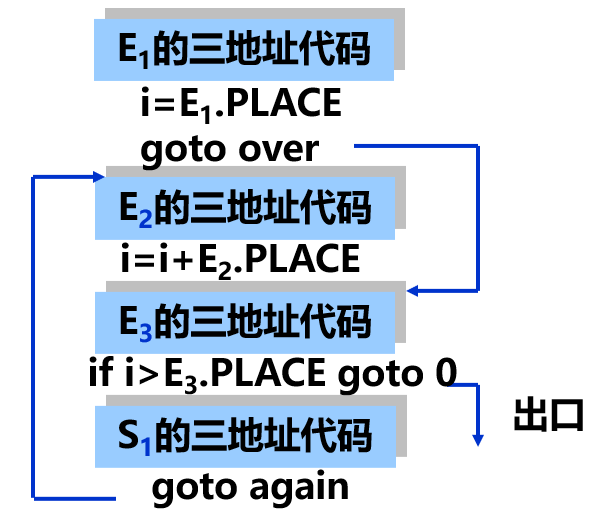
语义子程序为:

$F_1 \to for \ i:=E_1$

{
  P := entry(i.NAME);
  // 产生 i := E1
  emit(P, =, E1.PLACE);
  // 记录 i 的地址
  F1.PLACE := P;
  F1.CHAIN := ip;
  // 产生 goto over, 等待回填
  emit(j, 0);
  // 记录 again 地址
  F1.AGAIN := ip;
}

$F_2 \to F_1 \ step \ E_2$

{
  F2.AGAIN = F1.AGAIN;
  F2.PLACE = F1.PLACE;
  // 生成 i = i + E2
  emit(F2.PLACE, F2.PLACE, +, E2.PLACE);
  // 回填 over 地址
  backpatch(F1.CHAIN, ip);
}

$F_3 \to F_2 \ until \ E_3$

{
  F3.AGAIN := F2.AGAIN;
  F3.CHAIN := ip;
  // for 语句的出口语句
  emit(jnz, F2.PLACE, E3.PLACE, 0);
}

$S \to F_3 \ do \ S_1$

{
  // 产生 goto again
  emit(j, F3.AGAIN);
  // 设置 S1 出口为 again
  backpatch(S1.CHAIN, F3.AGAIN);
  S.CHAIN := F3.CHAIN;
}

调用过程的翻译

文法为:

\left\{ \begin{array}{l} S \to call \ i(arglist) \\ arglist \to arglist_1, E \\ arglist \to E \end{array} \right.

假定传参方式为引址调用.

主要考虑实参的放置位置:

最简单的方法: 把实参的地址放在转子指令前面.

语义子程序如下:

$arglist \to E$

{
  建立队列 arglist.QUEUE, 其只包含一项 E.PLACE;
  arglist.DIM := 1;
}

$arglist \to arglist_1, E$

{
  把 E.PLACE 加在 arglist1.QUEUE 的末端;
  arglist.DIM := arglist1.DIM + 1;
  arglist.QUEUE := arglist1.QUEUE;
}

$S \to call \ i(arglist)$

{
  for X := range arglist.QUEUE do emit(param X);
  emit(call, i.NAME, arglist.DIM);
}

代码优化和目标代码生成

局部优化

优化是一种等价和有效的程序变换.

等价: 不改变程序运行结果.

有效: 变换后的程序比变换前所占的空间更少, 执行速度更快.

不同阶段的优化

源程序阶段的优化: 考虑数据结构和算法.
编译优化: 中间代码优化和目标代码优化.
中间代码优化:
1. 局部优化: 在基本块内的优化.
2. 全局优化: 超越基本块, 在基本块之间的优化.

基本块

基本块: 基本块指程序中的一段语句(三地址语句)序列, 它只有一个入口语句, 即程序中该语句序列的第一个语句; 只有一个出口语句, 即该语句序列的最后一个语句.

基本块的划分如下:

入口语句:
- 程序的第一个语句.
- 能由转向语句(条件语句或者无条件语句)转移到的语句.
- 紧跟在条件语句之后的语句.
出口语句:
- 转向语句.
- 停止语句.
划分基本块的方法:
- 求出三地址语句序列中的各个入口语句.
- 对每个入口语句构造一个基本块(由入口语句到下一条入口语句, 或到一条转移语句/停止语句之间的语句序列组成).
- 删除未被纳入任何基本块的语句.

程序流图

程序流图(Program Flow Graph) 是程序结构的图形表示, 可形式化为 $G=(N, E, n_0)$ , 其中:

$N$ 是节点集, 即: 基本块集.
$E$ 是有向边的集合, 如果节点 $n_1$ 将控制转向节点 $n_2$ , 则有一条由 $n_1$ 指向 $n_2$ 的有向边.
首节点 $n_0$ 是包含程序第一条语句的节点.

构造程序流图的算法如下:

输入基本块集 $N$ .
含程序第一条语句的基本块为首节点 $n_0$ .
设 $B_i, B_j \in N$ $B_{i}, B_{j} \in N$ , 若满足条件:
1. $B_j$ 紧跟在 $B_i$ 之后, 且 $B_i$ 的出口不是无条件转移或者停止语句.
2. $B_i$ 的出口语句为转移语句, 且转移点为 $B_j$ 的入口语句.
  则 $B_i$ 和 $B_j$ 之间有一条有向边 $B_i \to B_j$ .

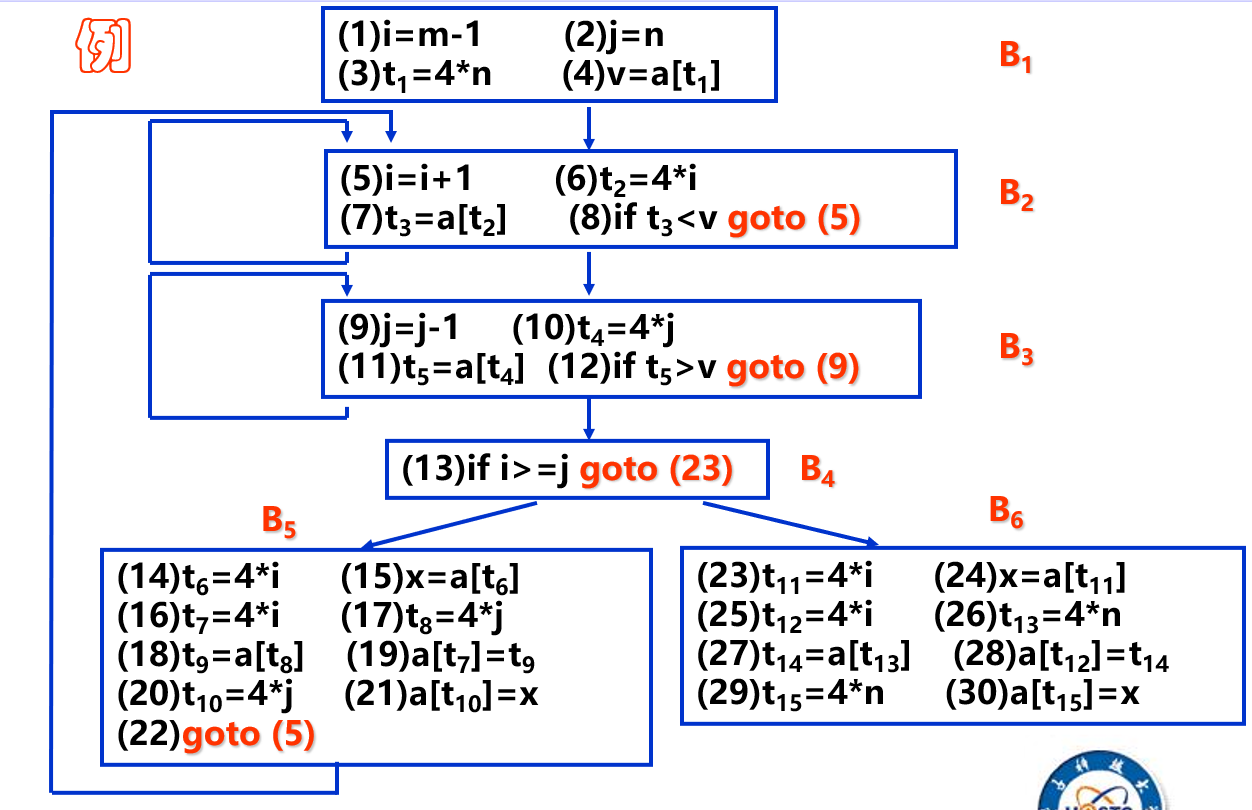
基本块内的优化

合并已知量

对于 A := OP B 或 A := B OP C 这样的语句, 如果 B, C 为常数, 则编译时可以将其计算出来, 把值存放到临时单元中, 相应的语句变为 A := T.

删除公共子表达式

也叫删除多余运算, 如两条赋值语句:

A := B + C * D;
U := V - C * D;

其中有两次 C * D 运算, 只计算一次, 将值存在临时单元 T 中, 第二个个语句改为 U := V - T;

删除无用赋值

例如四元式序列:

(p) A := B + D;
...
(q) A := M + N;

中没有对 A 的引用, 则第一个赋值无用, 可删除.

删除死代码

例如在 if B then S1 else S2 中, 如果 B 的值恒为 true 或者 false, 那么有一个分支永远不会执行, 可删除.

全局优化

全局优化有很多中, 这里只讨论循环优化.

循环的定义: 循环是程序流图中有唯一入口节点的强连通子图.

入口节点: 子图中满足下列条件的节点 $n$ $n$ :
- $n$ 是流图的首节点.
- 在子图外有一节点 $m$ , 它有一有向边 $m \to n$ 引向节点 $n$ .
强连通子图: 任意两个节点之间可以互相连通.

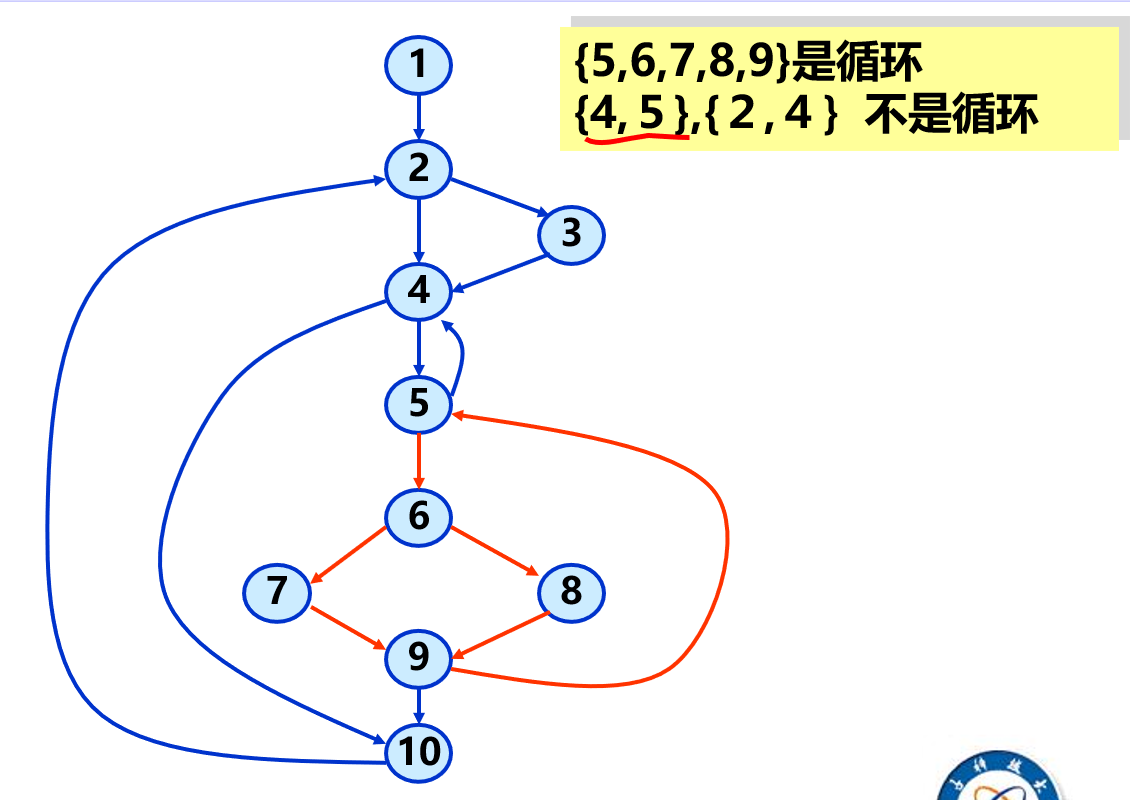
上图中, {4, 5} 有两个入口, {2, 4} 不是强连通子图.

必经节点集

必经节点: 从流图的首节点出发到达节点 $n$ 的任一通路都必须经过的节点 $d$ , 称为 $n$ 的必经节点, 记为 $d \ DOM \ n$ .

必经节点集: 流图中节点 $n$ 的所有必经节点的集合, 称为 $n$ 的必经节点集, 称为 $D(n)$ .

必经节点具有如下性质:

自反性: 对任意节点 $n$ , 有 $n \ DOM \ n$ .
传递性: 如果 $n_1 \ DOM \ n_2, n_2 \ DOM \ n_3$ , 则 $n_1 \ DOM \ n_3$ .
反对称性: 如果 $n_1 \ DOM \ n_2, n_2 \ DOM \ n_1$ , 则 $n_1 = n_2$ .

循环的查找

回边: 流图 $G=(N, E, n_0)$ 中的有向边 $n \to d$ , 如果 $d$ 是 $n$ 的必经节点, 即 $d \in D(n)$ , 则称 $n \to d$ 为流图的一条回边.

由回边构成的循环:

若 $n \to d$ 是该流图 $G=(N, E, n_0)$ 的一条回边, $M$ 是流图中有通路到达 $n$ 而该通路不经过 $d$ 的节点集, 则集合:

$LOOP = \{n,d\} \cup M$

组成了 $G$ 的一个子图, 称为由回边 $n \to d$ 组成的循环.

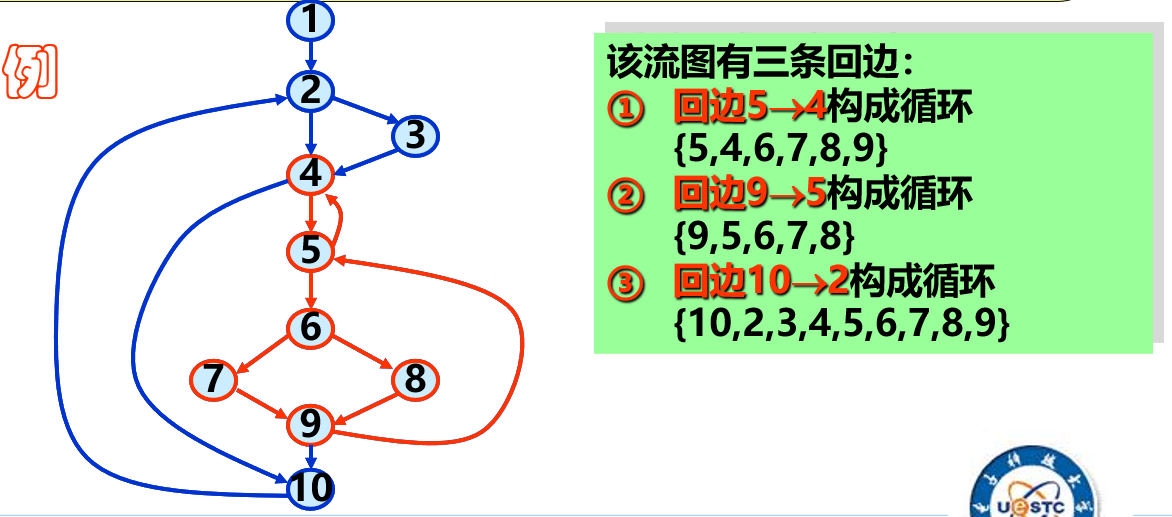
思考: $M$ 中的节点一定在节点 $n$ 之后吗? (如果在之前的话, 就必然经过必经节点 $d$ , 但是要求不经过 $d$ )

循环的优化

代码外提

在循环中, 对 x = op y 或 x = y op z 一类的运算, 如果 y, z 均为循环不变量, 则该代码可以提到循环外, 只计算一次.

强度削弱

在循环中, 如果变量 i 有唯一指定值 i = i + c, 则称 i 为基本归纳变量.

如果变量 j = c1 * i + c2, i 是基本归纳变量, 则称 j 为同族归纳变量.

将同组归纳变量 j 的乘法变成加法, 称为强度削弱, 即改成 j = j + c1 * c, 同时在循环外赋初始值 j = c1 * i + c2.

i 每个循环增加 c, j 每个循环增加 c1 * c, 即循环中: j += c1 * c, 初始值: j = c1 * i + c2.

删除归纳不变量

将循环的控制条件由依赖于基本归纳变量改为依赖同组归纳变量, 则可将基本归纳变量删除.

目标代码生成

将经过语法分析和语义分析后生成的中间代码, 或经过优化后的中间代码, 变换成目标代码, 称为目标代码生成.

目标代码通常有三种形式:

能够立即执行的机器语言代码.
带装配的机器语言模块, 需要连接程序与某些运行支持程序连接成目标程序, 由装入程序装入内存运行.
汇编语言代码, 需汇编程序汇编, 变换成可执行的机器语言代码.

目标代码生成的主要问题:

需要根据目标机的特性, 选择合适的指令, 生成最短的目标代码.
为了目标代码的有效性, 要充分利用目标机的寄存器.

后续目标代码生成的内容不涉及具体的机器.

一个计算机模型:

目标机具有多个通用寄存器, 可以作为变址器, 它的指令形如: OP src, dst.

指令模式有:

直接地址型:
- OP R_i, M
- $(R_i) \ OP \ (M) \Rightarrow R_i$
寄存器型:
- OP R_i, R_j
- $(R_i) \ OP \ (R_j) \Rightarrow R_i$
变址型:
- OP R_i, C(R_j)
- $(R_i) \ OP \ ((R_i) + C) \Rightarrow R_i$
间接型:
- OP R_i, *R_j
- $(R_i) \ OP \ (R_j) \Rightarrow R_i$
- OP R_i, *M
- $(R_i) \ OP \ (M) \Rightarrow R_i$
- OP R_i, *C(R_j)
- $(R_i) \ OP \ ((R_i) + C) \Rightarrow R_i$
寄存器到内存(只会把 R_i 中的值写回内存, 不会清除 R_i 中的值):
- MOV R_i, M
- $(R_i) \Rightarrow M$
内存到寄存器:
- MOV M, R_i
- $(M) \Rightarrow R_i$
转移:
- J X
- $goto X$

简单的代码生成方法

给定语句 $p$ : x = y op z, 其中 $p$ 是语句所在的位置, 这和语句一般由两条指令实现:

// 将 y 载入寄存器 R_i
MOV y, R_i
// 将寄存器 R_i 中的值与 z 进行 op 运算, 结果存入 R_i 中
OP R_i, z

为 x 分配寄存器, 要考虑如下三种情况:

y 本身占有寄存器 R_i, 且 y 在 p 点后不再被引用.
有空余的可用寄存器 R_i, 将 R_i 分配给 x, 生成上述两条指令.
寄存器均被占用: 保存副本, 选择一个--最好占用 R_i 的变量在主存中已经有副本的; 或者在 $p$ 点之后该变量不再被引用的; 或者在离 $p$ 点最远处才被引用的寄存器, 然后生成上述两条指令.

例:基本块中有如下指令:

t := a - b
u := a + c
v := a - t
w := v + u

假定可用寄存器为 R_0, R_1.

生成代码如下:

// R_0: a
MOV a, R_0

// R_0: t
SUB R_0, b

// R_1: c
MOV R_1, c

// R_1: u
ADD R_1, a

// Release R_1
MOV R_1, u

// R_1: a
MOV R_1, a

// R_1: v
SUB R_1, R_0

// Release R_1, 这里可以释放 R_0 吗?
MOV R_1, v

// R_1: w
ADD R_1, u

循环中的寄存器分配

由于访问寄存器比访问内存要快的多, 从全局来看, 将一定数量的寄存器固定分配给循环中频繁引用的变量, 是提高运行效率的一种策略.

如何知道给哪些变量固定分配寄存器收效最大?

指令的执行代价: 一条指令访问内存的次数.

寄存器型: op R_i, R_j 执行代价为 1(从内存到指令本身, 即取指, 代价为 1).
直接地址型: op R_i, M 执行代价为 2(取指 + 从内存读 M, 代价为 2).
变址型: op R_i, C(R_j) 执行代价为 2.
间接型:
- op R_i, *R_j: 执行代价为 2.
- op R_i, *M: 执行代价为 3.
- op R_i, *C(R_j) 执行代价为 3.

固定分配寄存器节省的代价计算:

如果变量固定占有寄存器, 则它在定值之前的每次引用就少一次访存, 即节省一个执行代价. 设 $USE(x, B)$ 为变量 x 在基本块 $B$ 中被定值前的引用次数, 则循环 $L$ 执行一次, 可节省的执行代价为: $\Sigma USE(x, B), B \in L$
对在基本块中定值的, 在基本块后的活跃变量 x, 如果对它固定分配寄存器, 则可省去指令 MOV R_i, M, 因此可以节省代价 2. 令 $LIVE(x, B) = 1$ 表示变量 x 在基本块 $B$ 后活跃, 则循环 $L$ 执行一次, 可省执行代价: $\Sigma 2 * LIVE(x, B), B \in L$ .

所以, 对变量 x 固定分配寄存器, 总共可节省执行代价: $\Sigma (USE(x, B) + 2 * LIVE(x, B)), B \in L$ .

运行时存储空间的组织

程序的存储空间

程序的代码空间

源程序经过编译后生成的目标代码的存储区域, 称为代码空间.
代码空间没有复杂的组织和管理问题, 执行次序由程序控制, 代码空间存放的代码在运行时不会改变.

假定当前指令指针 ip 的值为 i, 则当前指令的存储用 C[i] 表示.

程序的数据空间

编译程序给源程序中的各种类型的变量和常数分配的存储空间, 称为程序的数据空间.
数据空间在运行时是可以改变的, 即动态的.

若某个变量分配在数据存储器 D 的第 i 个单元, 则用 D[i] 表示该变量的存储地址.

数据空间的特点

初等数据类型通常以基本存储单元来存储. 聚合数据类型一般用相继的若干个字或者字节来存储.
变量获得存储区的活动称为存储分配.
数据空间除了变量和常数外, 还有一些控制和管理信息.
变量的属性影响其存储分配.
如果能在编译时, 使变量绑定在存储区, 称为静态分配策略; 如果必须在运行时才能完成存储分配, 叫做动态分配策略.

活动记录

程序单元的数据空间称为活动记录(Activation Record). 程序单元激活时所需的信息管理通过相应的活动记录来实施. 程序单元的每次激活, 都建立相应的活动记录, 它是单元实例的一部分. 一个活动记录是一个连续的存储区.

变量的存储分配

从存储的角度来看, 变量有四种类型:

静态变量: 活动记录以及变量的存储位置在编译时可以确定, 存储分配在编译时完成, 无论程序单元的哪一次激活, 变量都绑定于活动记录中相同的存储位置.
半静态变量: 语言允许递归调用, 每次激活分配相应的活动记录. 编译时确定相对位置 offset(x), 单元被激活后, 变量 x 绑定于 D + offset(x).
半动态变量: 编译时在活动记录中建立描述符, 描述符的大小在编译时可以确定, 在单元激活时, 才分配他们的空间.
动态变量: 描述符及空间大小在编译时不能确定, 编译时在活动记录中为动态变量设置 2 个指针, 一个指向该变量的描述符, 另一个指向该变量的存储空间.

存储分配模式

静态分配: 只允许静态变量, 变量与存储区域的绑定关系在编译时可以建立, 并完成存储分配. 不允许递归调用, 不允许动态数组, 不允许动态类型的数据对象, 即: 不允许有非静态变量.
栈式分配:
- 各单元之间的调用关系遵循后进先出的模式.
- 活动记录的建立和撤销也遵循后进先出的模式.
- 用栈分配活动记录.
- 活动记录的长度或者可以静态决定, 或者在单元激活时可以决定.
- 分配方法: 当激活一个程序单元时, 其活动记录就动态地分配于栈顶.
堆分配: 由于动态变量表示的数据对象的长度/个数都可能在执行中改变, 不可能在栈上作分配. 一般而言, 出现如下情况时, 必须用堆分配:
- 单元活动结束后, 局部变量的值还需要保留.
- 调用单元与被调用单元的生存期不满足嵌套关系, 即出现交叉现象.

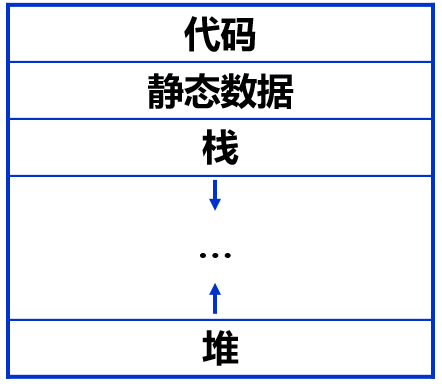
静态分配

早期的 FORTRAN 是典型的静态语言, 具有如下特点:

不允许过程的递归调用.
无动态数组和动态类型.
程序无嵌套层次结构.

...

栈式分配

栈式分配是动态分配.
支持语言的如下特征:
1. 允许过程的递归调用.
2. 允许动态数组.
3. 允许动态建立数据对象.
栈式分配的好处: 便于存储管理, 及时释放存储单元, 可以大大节省内存.

只含半静态变量的栈式分配

只允许过程的递归调用.
每个变量的长度静态可以确定.
每个程序单元的整个活动记录的长度可以静态决定.

分配原则:

每个活动记录在程序单元激活时建立在栈顶.
指针 current 指向活动记录的开始, 指针 free 指向栈顶的自由空间: free = current + L, L 为活动记录的长度.
局部单元通过指针 current 来引用.
程序单元退出时, 释放栈顶活动记录.

语句 call p 的翻译:

// 调用语句后 5 条语句为返回地址
D[free] := ip + 5
// 建立动态连接
D[free + 1] := current
// 将 current 调整到新建的活动记录
current := free
// 调整释放指针 free 到新的栈顶
free := free + L
// 控制转入被调用单元
ip := P的代码段首址

过程 p 返回指令的翻译:

// 释放 p 的当前活动记录
free := current
// 恢复调用单元的活动记录
current := D[current + 1]
// 将控制返回调用单元
ip := D[free]

被调用单元在活动记录中记录的调用单元的活动记录地址称为动态链接, 程序单元之间动态链接形成的链称为动态链.

半动态变量的栈式分配

只允许过程的递归调用.
允许使用像动态数组这样的半动态变量.
以动态数组为例进行动态分配.

要处理的问题:

活动记录的大小在编译时不能确定, 但数组的描述符大小(内情向量)大小可静态确定.

解决办法:

活动记录由两部分组成:

编译时可静态确定的部分.
动态数组的存储区.

实现办法:

程序单元被激活时, 在栈顶单元分配活动记录的第一部分, 分配后 free 指针指向栈顶.
遇到每个动态数组说明, 将确定的信息填入内情向量, 并计算出它的长度 L, 然后再栈顶分配 L 个空间, 即: free := free + L.

编译原理基础

# 编译原理基础

# 绪论

# 高级语言

# 强制式语言

# 数据类型

# 引言--数据类型

# 内部类型

# 用户定义的类型

# 笛卡尔积

# 有限映像

# 序列

# 递归

# 判定或

# 幂集

# PASCAL 语言数据类型结构

# PASCAL 非结构类型

# PASCAL 聚合构造

# PASCAL 记录构造

# PASCAL 文件构造

# PASCAL 指针

# C 语言数据类型结构

# C 非结构类型

# C 用户自定义的非结构类型

# C 聚合构造

# 抽象数据类型

# 类型检查

# 类型转换

# 类型等价

# 实现模型

# 内部类型和用户定义的非结构类型的实现模型

# 结构类型的实现模型

# 控制结构

# 语句级控制结构

# 顺序

# 选择

# 循环

# 语句级控制结构分析

# 单元级控制结构

# 显式调用

# 隐式调用

# 协同程序

# 并发单元

# 程序语言的设计

# 形式语言

# 术语

# 文法

# 语言

# 编译概述

# 基本概念

# 编译步骤

# 词法分析

# 词法分析概述

# 单词符号的类别

# 词法分析器的输出形式

# 词法分析器的设计

# 符号表

# 自上而下的语法分析

# 引言--自上而下的语法分析

# 回溯分析法

# 产生回溯的原因

# 消除回溯的方法

# 递归下降分析法

# 扩充的 BNF

# 预测分析法

# 预测分析表

# 预测分析器的执行算法

# 预测分析表的构造--集合

# 预测分析表的构造--算法

# 预测分析表的具体实现

# 自下而上的语法分析

# 引言--自下而上的语法分析

# 核心概念

# 短语

# 直接短语

# 句柄

# 素短语

# 最左素短语

# 利用推导树进行判断

# 算符优先分析法

编译原理基础

绪论

高级语言

强制式语言

数据类型

引言--数据类型

内部类型

用户定义的类型

笛卡尔积

有限映像

序列

递归

判定或

幂集

PASCAL 语言数据类型结构

PASCAL 非结构类型

PASCAL 聚合构造

PASCAL 记录构造

PASCAL 文件构造

PASCAL 指针

C 语言数据类型结构

C 非结构类型

C 用户自定义的非结构类型

C 聚合构造

抽象数据类型

类型检查

类型转换

类型等价

实现模型

内部类型和用户定义的非结构类型的实现模型

结构类型的实现模型

控制结构

语句级控制结构

顺序

选择

循环

语句级控制结构分析

单元级控制结构

显式调用

隐式调用

协同程序

并发单元

程序语言的设计

形式语言

术语

文法

语言

编译概述

基本概念

编译步骤

词法分析

词法分析概述

单词符号的类别

词法分析器的输出形式

词法分析器的设计

符号表

自上而下的语法分析

引言--自上而下的语法分析

回溯分析法

产生回溯的原因

消除回溯的方法

递归下降分析法

扩充的 BNF

预测分析法

预测分析表

预测分析器的执行算法

预测分析表的构造--集合

预测分析表的构造--算法

预测分析表的具体实现

自下而上的语法分析

引言--自下而上的语法分析

核心概念

短语

直接短语

句柄

素短语

最左素短语

利用推导树进行判断

算符优先分析法

算符文法