堆

堆是一个完全二叉树, 可以分为大根堆(MaxHeap)和小根堆(MinHeap).

我们以小根堆举例.

核心要点

堆的存储

使用数组存储堆, 由完全二叉树的特性:

1. x 节点的父节点为 (x - 1) / 2(注意 x 不为 0).
2. x 节点的子节点为 x * 2 + 1 和 x * 2 + 2.

int[] heap;
int size;

堆的基本操作

堆的基本操作包括两个:

1. down(x): 下移节点, 将其与子节点的最小值交换.
2. up(x): 上移节点, 如果值小于父节点, 就和父节点的值交换.

操作的时间复杂度为 $O(logN)$.

public void down(int x) {
  int t = x;
  int leftChild = x * 2 + 1;
  int rightChild = x * 2 + 2;

  if (leftChild < size && heap[t] > heap[leftChild]) t = leftChild;
  if (rightChild < size && heap[t] > heap[rightChild]) t = rightChild;

  if (t != x) {
    int temp = heap[t];
    heap[t] = heap[x];
    heap[x] = temp;

    down(t);
  }
}

public void up(int x) {
  if (x == 0) return;

  int parent = (x - 1) / 2;

  if (heap[x] < heap[parent]) {
    int temp = heap[x];
    heap[x] = heap[parent];
    heap[parent] = temp;

    up(parent);
  }
}

堆的扩展操作

堆的扩展操作都可以通过基础操作实现.

插入

public void insert(int x) {
  size++;
  // may expand heap array
  heap[size - 1] = x;
  up(size);
}

取最小

public int getMin() {
  return heap[0];
}

删除最小

public void deleteMin() {
  heap[0] = heap[size - 1];
  size--;
  down(0);
}

删除任何一个元素

public void delete(int x) {
  if (x >= size) return;

  heap[x] = heap[size - 1];
  size--;

  // either up or down will be executed, but not both.
  up(x);
  down(x);
}

修改任何一个元素

public void update(int x, int value) {
  heap[x] = value;
  up(x);
  down(x);
}

堆的创建

从 n / 2 处开始整理堆.

public void create(int[] arr) {
  size = 0;

  for (int i = 0; i < arr.length(); i++) {
    heap[i] = arr[i];
    size++:
  }

  for (int i = size / 2; i >= 0; i--) {
    down(i);
  }
}

例题

堆排序-acwing

堆排序-acwing

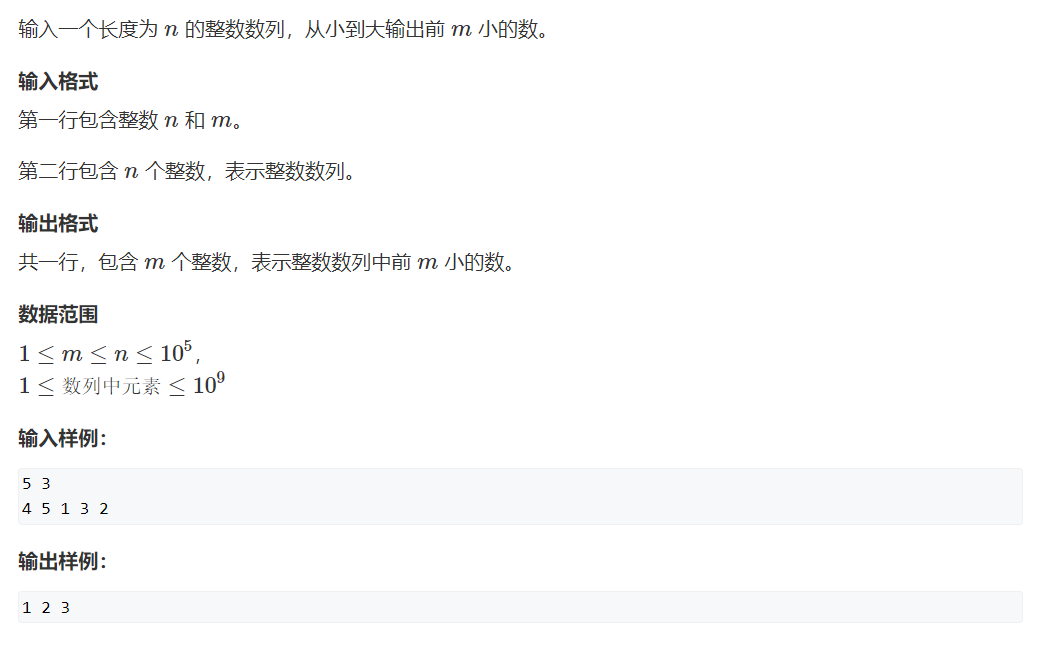
public class acwing_840 {

    static int[] heap = new int[10010];

    static int size = 0;

    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));


    public static void main(String[] args) throws IOException {
        String numsStr = reader.readLine();
        String[] nums = numsStr.split(" ");

        int n = Integer.parseInt(nums[0]);
        int m = Integer.parseInt(nums[1]);

        String itemsStr = reader.readLine();
        String[] items = itemsStr.split(" ");

        for (String item : items) {
            heap[size++] = Integer.parseInt(item);
        }

        for (int i = size / 2; i >= 0; i--) {
            down(i);
        }

        for (int i = 0; i < m; i++) {
            System.out.println(heap[0]);
            heap[0] = heap[size - 1];
            size--;
            down(0);
        }
    }

    static void down(int x) {
        int t = x;
        int leftChild = x * 2 + 1;
        int rightChild = x * 2 + 2;

        if (leftChild < size && heap[t] > heap[leftChild]) t = leftChild;
        if (rightChild < size && heap[t] > heap[rightChild]) t = rightChild;

        if (t != x) {
            int temp = heap[t];
            heap[t] = heap[x];
            heap[x] = temp;

            down(t);
        }
    }
}