SkipList(跳跃表)

Riicarus大约 8 分钟算法数据结构SkipList

SkipList(跳跃表)

SkipList 作为 Redis zset 的重要实现方式, 提供了很好的插入和删除性能, 同时在排序和搜索上也毫不逊色. 本文通过对一篇论文的阅读来理解 SkipList 的实现和优缺点.

论文: Skip Lists: A Probabilistic Alternative to Balanced Trees

Skip Lists: A Probabilistic Alternative to Balanced Treesopen in new window

Skip lists are data structures that use probabilistic balancing rather than strictly enforced balancing. As a result, the algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees.
跳跃表使用概率来保证平衡, 而不是严格使用强制平衡操作来保证(如平衡树). 因此, 相较平衡树的平衡算法来说, 跳跃表的插入和删除算法要简单和快捷很多.

平衡树

我们先来看看平衡树. 平衡树作为一个抽象数据结构, 被广泛用于字典和有序列表中. 当被插入元素是以随机顺序插入时, 平衡树的表现良好. 但如果以有序的顺序插入时, 平衡树的结构会退化为链表, 导致很多次的重新平衡操作, 性能很差. 平衡树算法在执行操作时重新排列树, 以保持一定的平衡状态并确保良好的性能. 由此我们发现, 平衡树处理插入序列中有序子序列较多的情况时表现不够好, 主要原因是有序子序列带来的很多次的重新平衡操作.

AVLTree
AVLTree

SkipList

再来看 SkipList.

对于一个(有序)链表来说, 搜索一个节点, 需要遍历整个树, 需要不超过 nn 次查找; 如果每个节点都有指向其后第二个节点的指针, 那么我们需要不超过 n/2+1n / 2 + 1 次查找; 如果每个节点再增加一个指向其后第四个节点的指针, 那么查找次数会变为不超过 n/4+2n / 4 + 2 次; 如果每个节点都维持指向其后第 2i2^i 个节点的指针, 那么查找次数会变为不超过 log⁡2n\log_2n 次. 由上, 我们使用增加向后的指针的方式, 将搜索的时间复杂度从 O(n)O(n) 成功降低至 O(log⁡n)O(\log n). 不过这样也会有问题: 如果链表长度为 nn, 那么我们需要为每个节点维护 log⁡2n\log_2 n 个指向后续节点的指针, 当 nn 非常大时, 这个维护成本会变得很高.

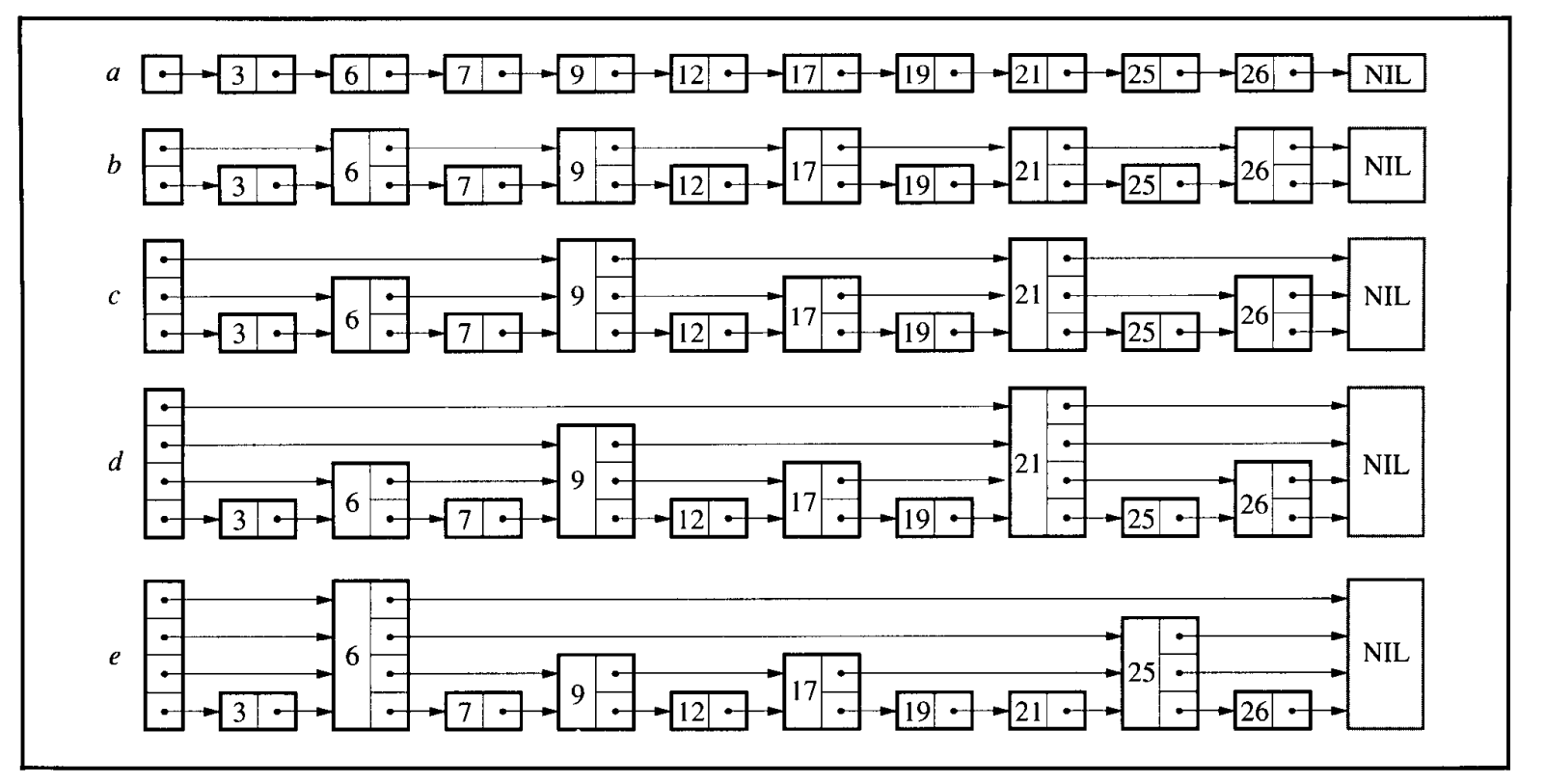
SkipList
SkipList

我们将一个具有指向其后 nn 个节点的指针的节点称为 nn 层节点. 如果每 2i2^i 个节点都有指向其后第 2i2^i 个节点的指针, 那么每层节点会有如下的简单分布:

  • 第 1 层节点: 50%
  • 第 2 层节点: 25%
  • 第 3 层节点: 12.5%
  • ...

但是这样会使得链表结构被束缚住(每层间距必须相等), 和平衡树面临的问题类似了. 那如果我们保持这个分布概率, 但是让每一层节点随机分布; 节点的第 ii 层指针不需要一定指向其后第 2i2^i 个节点, 而是指向下一个同层或更高层的节点; 节点的层数由插入前随机选择; 这样的话, 我们能够在绝大多数情况下得到 O(log⁡n)O(\log n) 的复杂度, 而不被之前的结构束缚.

SkipList 相关算法

SkipList 相较于普通的 LinkedList, 不同的算法主要包括初始化, 插入/删除和搜索.

结构

  • 每个元素用节点来抽象, 节点的层数是随机产生的.
  • 第 nn 层节点拥有从 1 到 nn 层的指针.
  • 链表的最大层数被设置为一个常数 MaxLevel
  • 链表只保存当前的最高层数为 level.
  • 链表的头节点拥有从 1 到 level 层的指针, 分别指向后续节点或者尾节点.
  • 链表的尾节点从 1 到 level 层的指针, 分别由前驱节点或者头节点指向, 被命名为 NIL. 所有层的节点最终都会指向 NIL.

初始化

SkipList 的 level 被设置为 1, 初始化 NIL 尾节点, 将头节点指向 NIL.

搜索

从头节点开始, 由高层向底层搜索, 先从高层迅速迭代, 如果高层不能继续迭代, 就下降一层, 由此循环直到第一层遍历结束. 此时停止的节点, 要么是要寻找的节点, 要么就是链表中不存在对应的元素.

func (l *SkipList) Search(searchKey int) (int, error) {
    x := l.header

    // 这里会一直迭代到第一层 key 最大但是不大于 searchKey 的节点
    for i := l.level; i > 0; i-- {
        for ; x.forward[i].key < searchKey; x = x.forward[i] {}
    }

    // 必定是下一个节点
    x := x.forward[1]

    if x.key != searchKey {
        return 0, SkipList.NIL
    }

    return x.value, nil
}

插入/删除

为了找到要插入或者删除元素的位置, 我们需要先使用 Search() 的逻辑来获得位置信息. 然后插入/删除对应的节点, 更新相关的元素(每一层需要更新的指针, 使用 update 表示). 如果插入节点的层数大于当前链表的最大层数, 那么需要更新链表的最大层数 level.

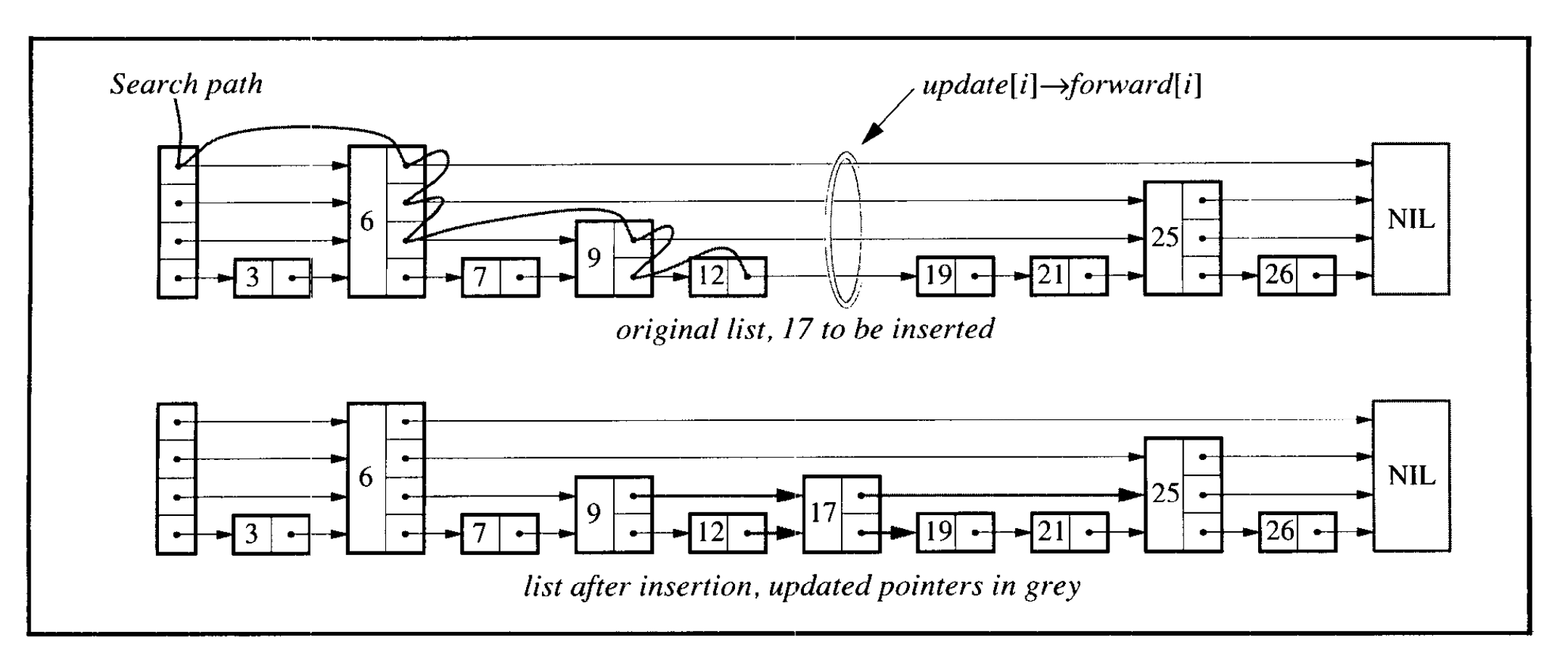
SkipListSearchProcess
SkipListSearchProcess
func (l *SkipList) Insert(searchKey, newValue int) {
    update := make([]*Node, MaxLevel)

    x := l.header
    for i := l.level; i > 0; i-- {
        for ; x.forward[i].key < searchKey; x = x.forward[i] {}
        update[i] = x
    }
    x := x.forward[1]

    if x.key = searchKey {
        x.value = newValue
        return
    }

    newLevel := randomLevel()
    if newLevel > l.level {
        for i := l.level + 1; i <= newLevel; i++ {
            update[i] = l.header
    }
        l.level = newLevel
    }

    x := makeNode(newLevel, searchKey, newValue)
    for i := 1; i <= newLevel; i++ {
        x.forward[i] = update[i].forward[i]
        update[i].forward[i] = x
    }
}

func (l *SkipList) Delete(searchKey int) (int, error) {
    update := make([]*Node, MaxLevel)

    x := l.header
    for i := l.level; i > 0; i-- {
        for ; x.forward[i].key < searchKey; x = x.forward[i] {}
        update[i] = x
    }
    x := x.forward[1]

    if x.key = searchKey {
        for i := 1; i <= l.level; i++ {
            if update[i].forward[i] != x {
                break
            }
            update[i].forward[i] = x.forward[i]
        }

        // 由上到下清除不需要的层
        for ;l.level > 1; {
            if l.header.forward[l.level] = NILNode {
                l.level--
            }
        }

        return x.value, nil
    }

    return 0, SkipList.NIL
}

func randomLevel() int {
    newLevel := 1
    for ; random() < p; newLevel++ {}

    return min(newLevel, MaxLevel)
}

从哪里开始搜索?

在上面的算法中, 我们简单的从最高层开始搜索. 但是我们可以考虑一个极端情况:
如果 MaxLevel 设置为 32, 链表中有 16 个元素, randomLevel() 中 p 设置为 1/2, 可能有如下情况: 第 1 层有 9 个元素; 第 2 层有 3 个元素; 第 3 层有 3 个元素; 第 14 层有 1 个元素. 如果从最高层开始搜索, 就会做很多次无意义的迭代.

那我们应该从哪个地方开始搜索呢? 论文分析中指出, 应该从 L(n)=log⁡1/pnL(n) = \log_{1/p}n (nn 为节点个数)开始. 对于此, 我们有如下解决方案:

  • 直接不管, 从最高层莽就完了. 极端情况之所以为极端情况, 就是因为发生概率极小, 而且我们可以从上述情况推测出, 这种极端情况出现在 MaxLevel 远大于当前数据量需要的层数时. 而在实际应用中, 对于大量数据的处理基本不会有这种情况发生(本身数据量大, 就需要较大的 MaxLevel); 对于少量数据的处理, 极端情况带来的多余迭代操作控制在很小的常数级, 用不着关心.
  • 从更小的层数开始. 直接通过 L(n)L(n) 计算出开始层数, 然后由此向下遍历. 但是这样为每次的操作都进行计算, 只是为了减少概率极小的情况, 性能反而降低很多.
  • 消除空层. 当待添加节点的 newLevel 大于 l.level 的时候, 将 newLevel 和 l.level 都设置为 l.level + 1, 这样就不会出现空层. 但是, 每次只增加一层, 会破坏随机性, 应该避免此类操作.

MaxLevel 如何确定?

由公式 L(n)=log⁡1/pnL(n) = \log_{1/p}n, 确定 MaxLevel=⌈L(n)⌉MaxLevel = \lceil L(n) \rceil. 如: p=1/2,MaxLevel=16p = 1/2, MaxLevel = 16, 可以保存 2162^{16} 个数据.

Redis 中 SkipList 的 MaxLevel 为 32.

Redis SkipList

定义

Redis 中, zset 的底层实现包括 ziplist 和 skiplist, 当元素数量大于 128 个或者元素大小大于 64 字节时, 就会使用 skiplist 来实现. 与上面论文讲述不同, Redis 允许有相同的 key 存在, 因此会增加对 value 是否相等的判断逻辑. 同时, 每个节点还增加了一个跨度为 1 的后退指针, 由表尾向表头迭代, 用于进行逆序操作. 对于每层前进指针, 不止保存下一个元素的指针, 还会保存当前层跨域的节点数量, 用于进行一些区间操作.

redis.h/zskiplist 定义跳跃表结构:

typedef struct zskiplist {

    // 头节点，尾节点
    struct zskiplistNode *header, *tail;

    // 节点数量
    unsigned long length;

    // 目前表内节点的最大层数
    int level;

} zskiplist;

redis.h/zskiplistNode 定义跳跃表节点:

typedef struct zskiplistNode {

    // member 对象
    robj *obj;

    // 分值
    double score;

    // 后退指针
    struct zskiplistNode *backward;

    // 层
    struct zskiplistLevel {

        // 前进指针
        struct zskiplistNode *forward;

        // 这个层跨越的节点数量
        unsigned int span;

    } level[];

} zskiplistNode;

使用

SkipList 的使用目的很简单, 就是实现有序数据集.
zset 可以用于集合排序/延时队列/Top K/范围查找等场景.