多重背包问题

多重背包问题是 01 背包问题的变种, 每个物品可以选择 0 ~ s 次, 枚举复杂度更高, 因此需要进行优化.

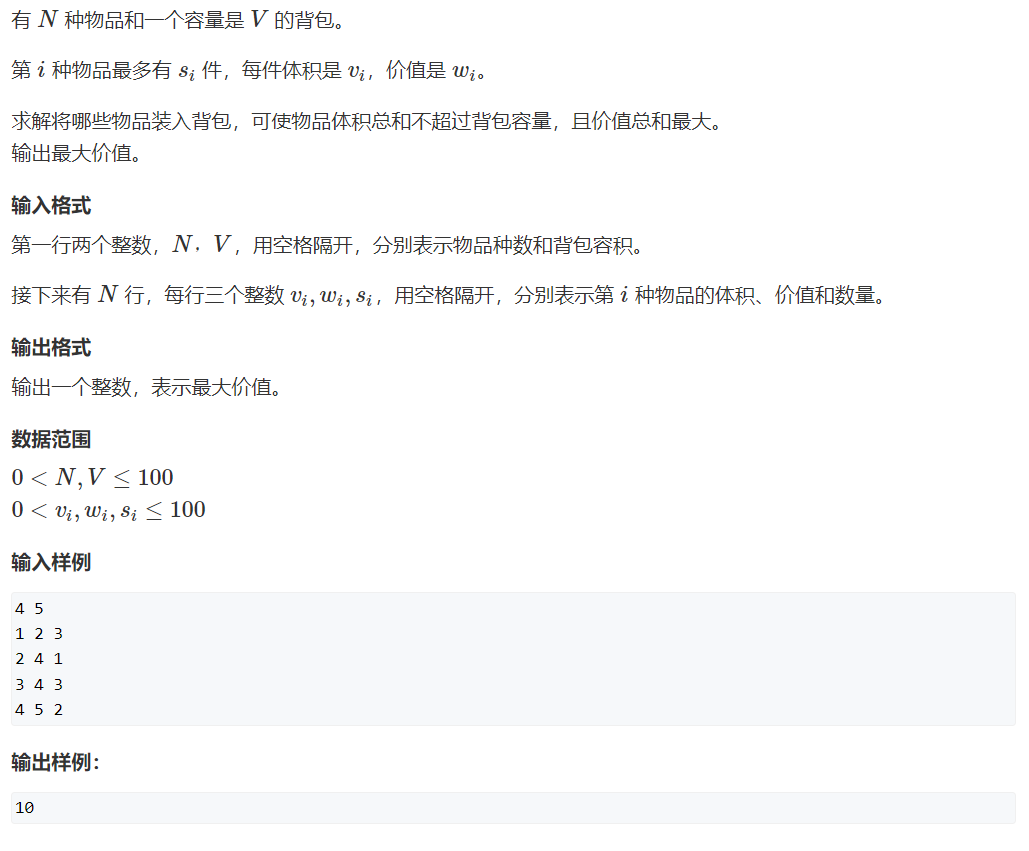
例题

多重背包问题-acwing

多重背包问题-acwing

状态转移分析

由于每个物品可以选择 0 ~ s 个, 因此每个状态可能有 s + 1 种情况.

状态转移方程为: f(i, j) = max(f(i - 1, j), f(i - 1, j - v_i) + w_i, f(i - 1, j - 2 * v_i) + 2 * w_i, ..., f(i - 1, j - s_i * v_i) + s_i * w_i).

根据 01 背包问题的优化方法, 可以将转移方程优化为: f(j) = max(f(j), f(j - v_i) + w_i, f(j - 2 * v_i) + 2 * w_i, ..., f(j - s_i * v_i) + s_i * w_i).

但是这样只是压缩了空间, 时间复杂度同样为 $O(n^3)$.

public class acwing_4 {

    static final int N = 2010;

    static int[] f_op = new int[N];

    static int[] v = new int[N];
    static int[] w = new int[N];
    static int[] s = new int[N];

    static int n, m;

    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

    public static void main(String[] args) throws IOException {
        String numsStr = reader.readLine();
        String[] nums = numsStr.split(" ");
        n = Integer.parseInt(nums[0]);
        m = Integer.parseInt(nums[1]);

        for (int i = 1; i <= n; i++) {
            String numsStr_vw = reader.readLine();
            String[] nums_vw = numsStr_vw.split(" ");
            v[i] = Integer.parseInt(nums_vw[0]);
            w[i] = Integer.parseInt(nums_vw[1]);
            s[i] = Integer.parseInt(nums_vw[2]);
        }

        for (int i = 1; i <= n; i++) {
            for (int j = m; j >= v[i]; j--) {
                for (int k = 0; k * v[i] <= j && k <= s[i]; k++) {
                    f_op[j] = Math.max(f_op[j], f_op[j - k * v[i]] + k * w[i]);
                }
            }
        }

        System.out.println(f_op[m]);
    }
}

二进制数组优化

每个物品有 s 个, 我们可以将其看作: 有 s 种对应物品, 每个物品有一个, 可选可不选.

但是这样仍然没有降低复杂度, 我们考虑如何用更少的数量来完全列举 s 种物品.

例1: 用几个数之和(每个数字只能选择一次或者不选)可以列举 0 ~ 7 中的所有数字?

答案: 1 2 4

分析: 可以看出, 我们能够使用一个二进制数组的方式, 来列举任何数字, 使得复杂度从 $O(n)$ 降低为 $O(logN)$.

例2: 如果要列举 0 ~ 10 中的所有数字呢?

答案: 1 2 4 3

分析: 将 0 ~ 10 拆分为可以用二进制数组完全列举的元素 0 ~ 7, 再加上一个剩余的后缀 3, 就可以用 1, 2, 4 完全列举出来.

因此, 对于任意数 s, 完全列举 s 的二进制数组为:

$(s - 2^{\lfloor logS \rfloor}) + \sum_{i = 0}^{\lfloor logS \rfloor}{2^i}$

public class acwing_4 {

    static final int N = 2010;

    static int[] f_op = new int[N];

    static int n, m;

    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

    record Item(int v, int w) {}

    public static void main(String[] args) throws IOException {
        String numsStr = reader.readLine();
        String[] nums = numsStr.split(" ");
        n = Integer.parseInt(nums[0]);
        m = Integer.parseInt(nums[1]);

        List<Item> items = new ArrayList<>();

        for (int i = 1; i <= n; i++) {
            int v, w, s;

            String numsStr_vw = reader.readLine();
            String[] nums_vw = numsStr_vw.split(" ");
            v = Integer.parseInt(nums_vw[0]);
            w = Integer.parseInt(nums_vw[1]);
            s = Integer.parseInt(nums_vw[2]);

            // 将 s 个物品当作 log(s) + 1 种物品.
            for (int j = 1; j <= s; j *= 2) {
                s -= j;
                items.add(new Item(v * j, w * j));
            }

            if (s != 0) {
                items.add(new Item(v * s, w * s));
            }
        }

        for (Item item : items) {
            for (int j = m; j >= item.v; j--) {
                f_op[j] = Math.max(f_op[j], f_op[j - item.v] + item.w);
            }
        }

        System.out.println(f_op[m]);
    }
}