01背包问题

例题

01背包-acwing

01背包-acwing

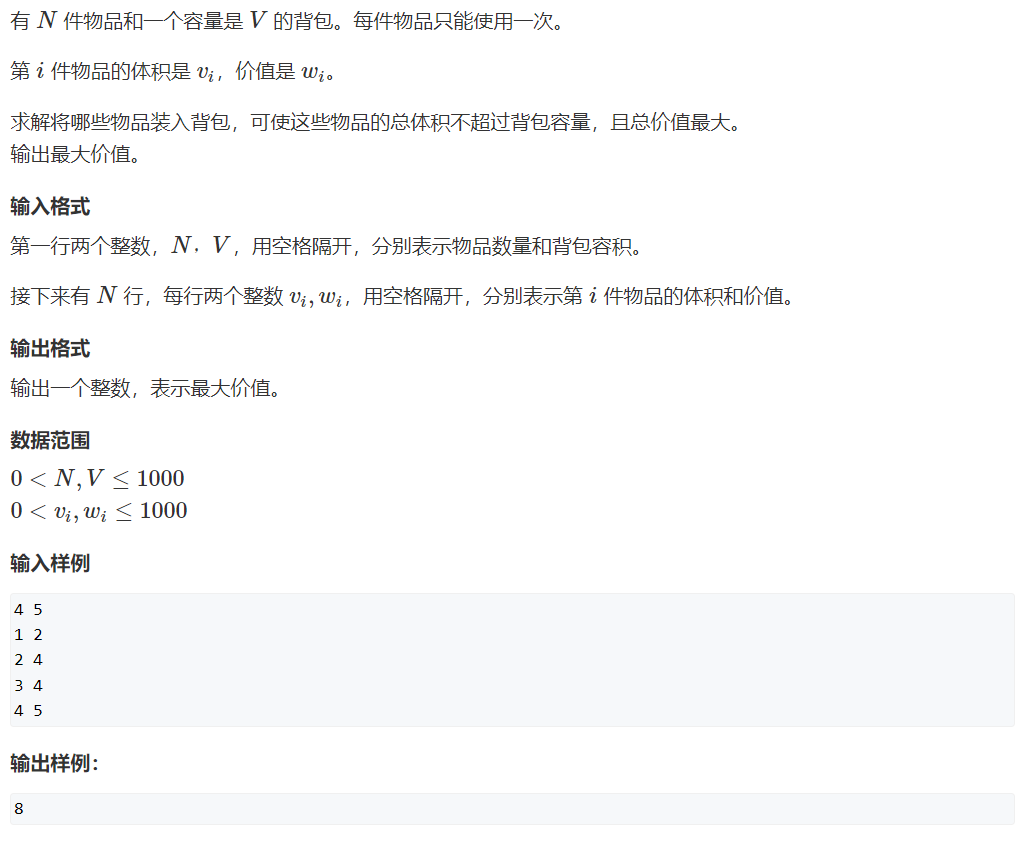
动态规划--闫氏分析法

以例题为例:

1. 状态表示: f(i, j)
   1. 集合: 所有只考虑前 i 个物品, 且总体积不超过 j 的选法的集合.
   2. 属性: Max/Min
2. 状态计算:
   1. 划分: 将 f(i, j) 对应的选择方案进行划分, 做到不重复, 不遗漏.
   2. 计算状态: 根据划分选择最合适(根据属性要求)的方案作为最优选择, 计算 f(i, j) 对应的状态.

对于例题而言, 状态 f(i, j) 计算流程为:

状态划分为:

1. 不选第 i 个物品.
2. 选第 i 个物品.

如果不选第 i 个物品, 那么 f(i, j) 就表示只考虑前 i - 1 个物品, 且总体积不超过 j 的选法的集合. 也就是 f(i - 1, j).

如果选第 i 个物品, 那么 f(i, j) 包括两个部分, 不变的部分为第 i 个物品的价值和体积, 变化的部分为前 i - 1 个物品的价值和体积, 即 f(i - 1, j - v_i). 所以, 这里 f(i, j) = f(i - 1, j - v_i) + w_i.

最后计算状态为两种情况的最大值, 即: f(i, j) = max(f(i - 1, j), f(i - 1, j - v_i) + w_i).

public class acwing_2 {

    static int[][] f = new int[1010][1010];
    static int[] v = new int[1010];
    static int[] w = new int[1010];

    static int n, m;

    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

    public static void main(String[] args) throws IOException {
        String numsStr = reader.readLine();
        String[] nums = numsStr.split(" ");
        n = Integer.parseInt(nums[0]);
        m = Integer.parseInt(nums[1]);

        for (int i = 1; i <= n; i++) {
            String numsStr_vw = reader.readLine();
            String[] nums_vw = numsStr_vw.split(" ");
            v[i] = Integer.parseInt(nums_vw[0]);
            w[i] = Integer.parseInt(nums_vw[1]);
        }

        // 从第一个物品开始
        for (int i = 1; i <= n; i++) {
            // 体积可以为 0
            for (int j = 0; j <= m; j++) {
                f[i][j] = f[i - 1][j];

                // 注意要保证之前有足够的空间可以不选 i
                if (j >= v[i]) f[i][j] = Math.max(f[i][j], f[i - 1][j - v[i]] + w[i]);
            }
        }

        System.out.println(f[n][m]);
    }
}

空间优化

由于状态转移的表达式只涉及到状态数组的第 i 层和第 i - 1 层, 那么状态数组只需要维护两层, 可以使用滚动数组.

考虑忽略 i, 只用 f(j) 来表示, 下面讨论其可能性.

同时, 根据分析不选 i 物品时, f(i, j) = f(i - 1, j); 选 i 物品时, 如果 j 从大到小遍历, f(i, j - v_i) 还没有被更新, f(i, j - v_1) 的值与 f(i - 1, j - v_i) 相同, 因此可以忽略状态数组中的 i 项.

最后的状态转移表达式为: f(j) = max(f(j), f(j - v_i) + w_i).

static int[] f_op = new int[1010];

for (int i = 1; i <= n; i++) {
    for (int j = m; j >= v[i]; j--) {
        f_op[j] = Math.max(f_op[j], f_op[j - v[i]] + w[i]);
    }
}