完全背包问题

完全背包问题的分析和 01 背包问题相似, 只是在状态转移和优化上不同.

例题

完全背包问题-acwing

完全背包问题-acwing

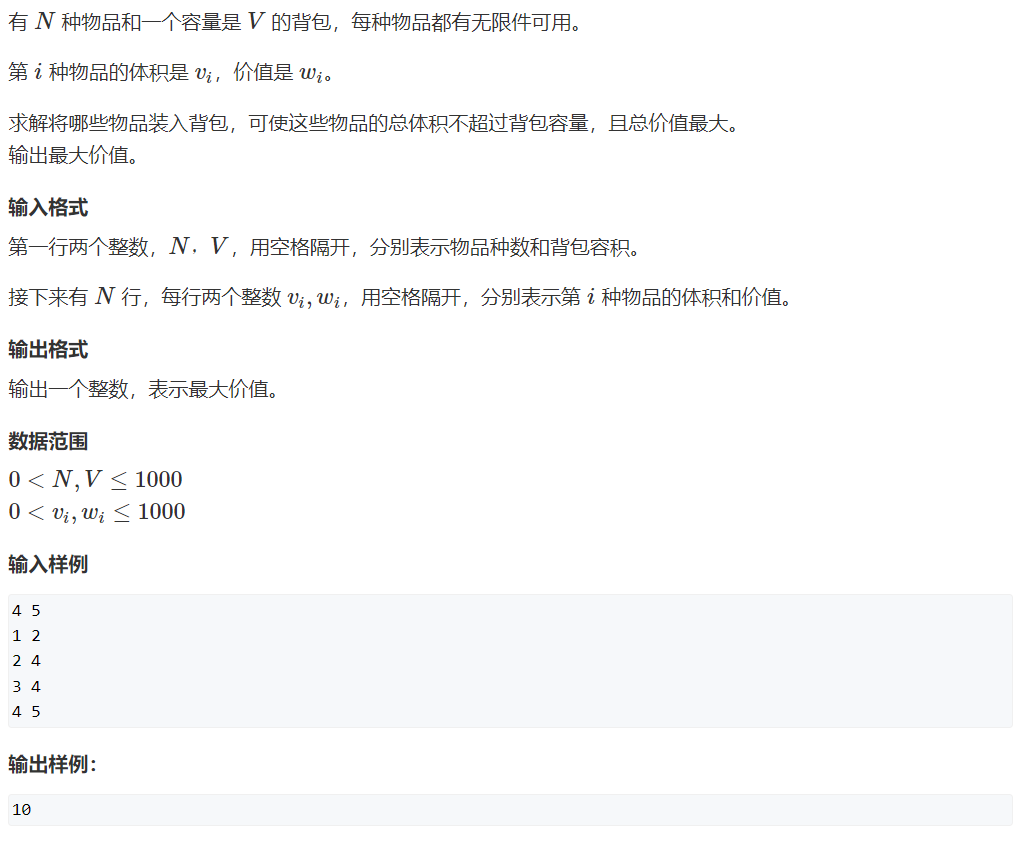
状态转移分析

对于第 i 个物品, 可以选择取 0 ~ k 个, 因此, f(i, j) = max(f(i - 1, j), f(i - 1, j - k * v_i) + k * w_i).

public class acwing_3 {

    static int[][] f = new int[1010][1010];
    static int[] v = new int[1010];
    static int[] w = new int[1010];

    static int n, m;

    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

    public static void main(String[] args) throws IOException {
        String numsStr = reader.readLine();
        String[] nums = numsStr.split(" ");
        n = Integer.parseInt(nums[0]);
        m = Integer.parseInt(nums[1]);

        for (int i = 1; i <= n; i++) {
            String numsStr_vw = reader.readLine();
            String[] nums_vw = numsStr_vw.split(" ");
            v[i] = Integer.parseInt(nums_vw[0]);
            w[i] = Integer.parseInt(nums_vw[1]);
        }

        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= m; j++) {
                for (int k = 0; k * v[i] <= j; k++) {
                    f[i][j] = f[i - 1][j];
                    f[i][j] = Math.max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
                }
            }
        }

        System.out.println(f[n][m]);
    }
}

优化

移项消除

$$\left\{ \begin{array}{l} f(i, j) = max(f(i - 1, j), \; f(i - 1, j - v_i) + w_i, \; f(i - 1, j - 2v_i) + 2w_i, ...) \\ f(i, j - v_i) = max(f(i - 1, j - v_i), \; f(i - 1, j - 2v_i) + w_i, \; f(i - 1, j - 3v_i) + 2w_i, ...) \\ \end{array} \right. \\ \Downarrow \\ f(i ,j) = max(f(i - 1, j), \; f(i, j - v_i) + w_i)$$

空间优化

注意, 我们为了将状态数组中的 i 项消除, 需要使 f(i - 1, j) 和 f(i, j - v_i) 与压缩后的 f(i, j) 和 f(i, j - v_i) 相同. 因此, 需要使 y 从小到大开始遍历.

static int[] f_op = new int[1010];

for (int i = 1; i <= n; i++) {
    for (int j = v[i]; j <= m; j++) {
        f_op[j] = Math.max(f_op[j], f_op[j - v[i]] + w[i]);
    }
}