最长上升子序列

例题

最长上升子序列-acwing

最长上升子序列-acwing

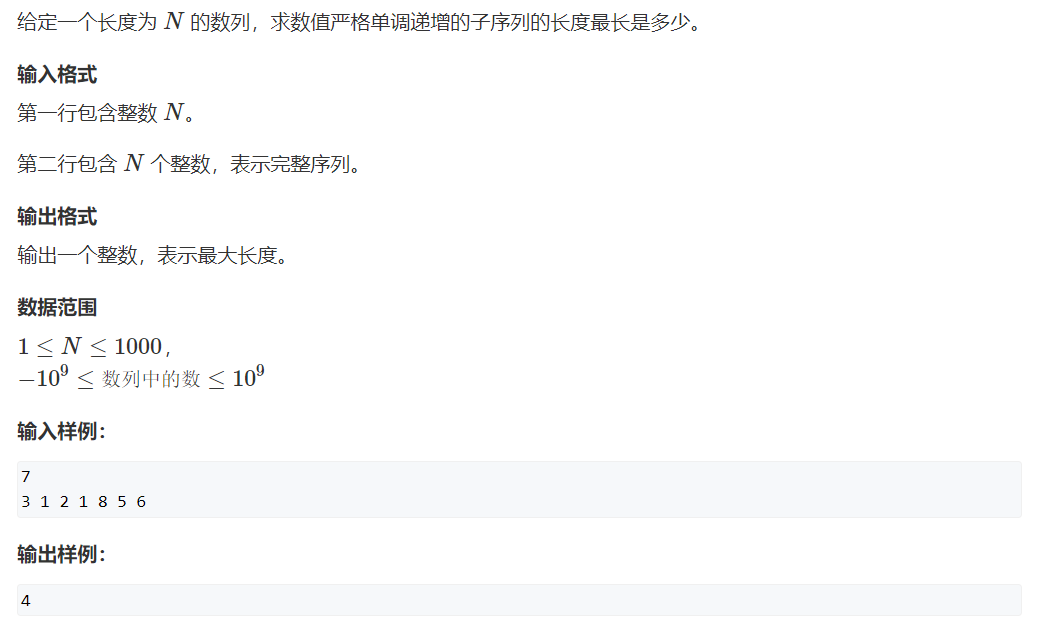
状态分析

用 f(i) 表示以第 i 个数字结尾的最长单调递增子序列的长度, 那么, 转移方程为:

f(i) = max(f(0), f(1), ..., f(i - 1)) + 1

public class acwing_895 {

    static int N = 1010;
    static int[] a = new int[N];
    static int[] f = new int[N];

    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

    public static void main(String[] args) throws IOException {
        int n = Integer.parseInt(reader.readLine());

        String[] nums = reader.readLine().split(" ");
        for (int i = 0; i < n; i++) {
            a[i] = Integer.parseInt(nums[i]);
        }

        Arrays.fill(f, 1);

        for (int i = 1; i < n; i++) {
            for (int j = i - 1; j >= 0; j--) {
                // 如果当前序列已经大于剩余元素的长度, 停止遍历
                if (f[i] > j + 1) break;

                // 如果是上升子序
                if (a[i] > a[j]) {
                    f[i] = Math.max(f[i], f[j] + 1);
                }
            }
        }

        int max = 1;
        for (int i : f) {
            max = Math.max(max, i);
        }

        System.out.println(max);
    }
}

优化

将数据范围扩展到 $1 \leq N \leq 100000$, 此时不能使用以上的方法, 会超时.

回顾以上的状态转移过程, 我们发现: 在 i - 1 到 0 中, 有一些最大的子序列的长度是相同的, 而我们对他们都遍历了一次, 可以将这个集合(具有相同最大子序列长度的元素的集合)用其对应的最大子序列长度来表示. 对于相同长度的最大子序列, 我们希望其结尾元素越小越好.

由此可以得出一个推论: 随最大子序列长度增大, 其对应的结尾元素的最小值单调递增.

这样, 我们可以使用二分法来寻找最大长度的字串, 其结尾元素不大于 a[i].

我们维护一个栈(或者类似的), 栈的高度与最大字串长度成正比, 栈顶为当前最大字串长度对应的结尾元素的值.

• 如果 a[i] 大于栈顶元素, 就将 a[i] 放入栈顶.
• 如果 a[1] 不大于栈顶元素, 就在栈中二分找到第一个大于等于 a[i] 的元素, 将其值改为 a[i].

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class acwing_896 {

    static int N = 100010;
    static long[] a = new long[N];
    static long[] f = new long[N];
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

    static int cnt = 0;

    public static void main(String[] args) throws IOException {
        int n = Integer.parseInt(reader.readLine());

        String[] nums = reader.readLine().split(" ");
        for (int i = 1; i <= n; i++) {
            a[i] = Long.parseLong(nums[i - 1]);
        }

        // 这里改的已经不是 DP 的转移方程了
        f[++cnt] = a[1];
        for (int i = 2; i <= n; i++) {
            if (a[i] > f[cnt]) f[++cnt] = a[i];
            else {
                int temp = search(a[i]);
                f[temp] = a[i];
            }
        }

        System.out.println(cnt);
    }

     static int search(long x) {
        int l = 1;
        int r = cnt;

        while (l < r) {
            int mid = l + r >> 1;
            if (f[mid] >= x) r = mid;
            else l = mid + 1;
        }

        return l;
    }

}