最短编辑距离

例题

最短编辑距离-acwing

最短编辑距离-acwing

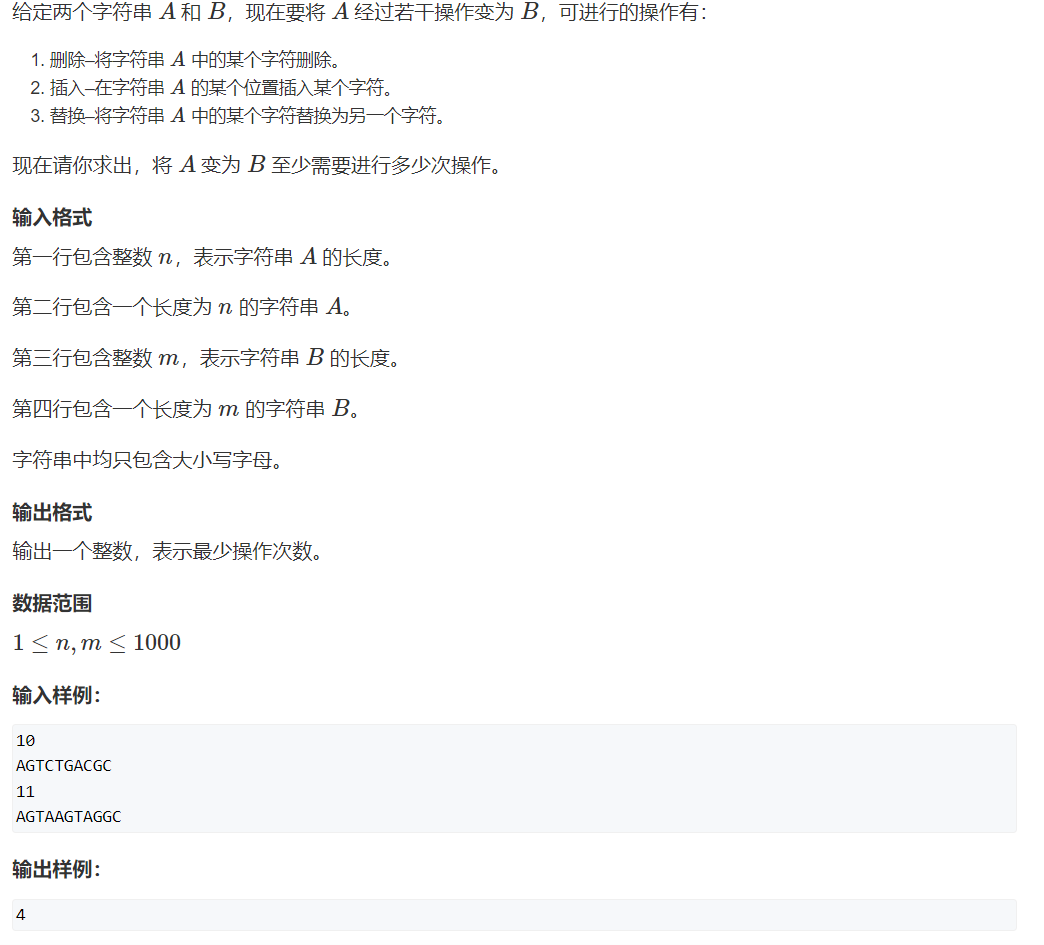
状态分析

使用 f(i, j) 表示从 A[1 ~ i] 变为 B[1 ~ j] 需要进行的操作次数, 属性为 MIN.

转移到 f(i, j) 的状态有三种, 以操作 A 字符串为例:

1. 操作到 i, j 时, A[i] 比 B[j] 长一个元素, 此时需要删除 A[i]. f(i, j) = f(i - 1, j) + 1.
2. 操作到 i, j 时, A[i] 比 B[j] 短一个元素, 此时需要删除 B[j]. f(i, j) = f(i, j - 1) + 1.
3. 操作到 i, j 时, A[i] 和 B[j] 长度相同, 此时需要将 A[i] 改为 B[j].
   1. 如果 A[i] == B[j]: f(i, j) = f(i - 1, j - 1).
   2. 如果 A[i] != B[j]: f(i, j) = f(i - 1, j - 1) + 1.

public class acwing_902 {

    static int N = 1010;
    static int[][] f = new int[N][N];

    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

    public static void main(String[] args) throws IOException {
        int n = Integer.parseInt(reader.readLine());
        String s1 = reader.readLine();

        int m = Integer.parseInt(reader.readLine());
        String s2 = reader.readLine();

        // 处理一个字符串为 0 的情况, 操作数一定等于另一个字符串的长度.
        for (int i = 0; i <= m; i++) {
            f[0][i] = i;
        }
        for (int i = 0; i <= n; i++) {
            f[i][0] = i;
        }

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                f[i][j] = Math.min(f[i - 1][j], f[i][j - 1]) + 1;

                if (s1.charAt(i - 1) == s2.charAt(j - 1)) f[i][j] = Math.min(f[i][j], f[i - 1][j - 1]);
                else f[i][j] = Math.min(f[i][j], f[i - 1][j - 1] + 1);
            }
        }

        System.out.println(f[n][m]);
    }
}

类似题目

编辑距离-acwing