数字三角形

数字三角形是一个经典的线性 DP 问题.

线性 DP

线性 DP 即 DP 中状态转移方程(求解状态的顺序)有明显的线性关系的一类问题.

例题

数字三角形-acwing

数字三角形-acwing

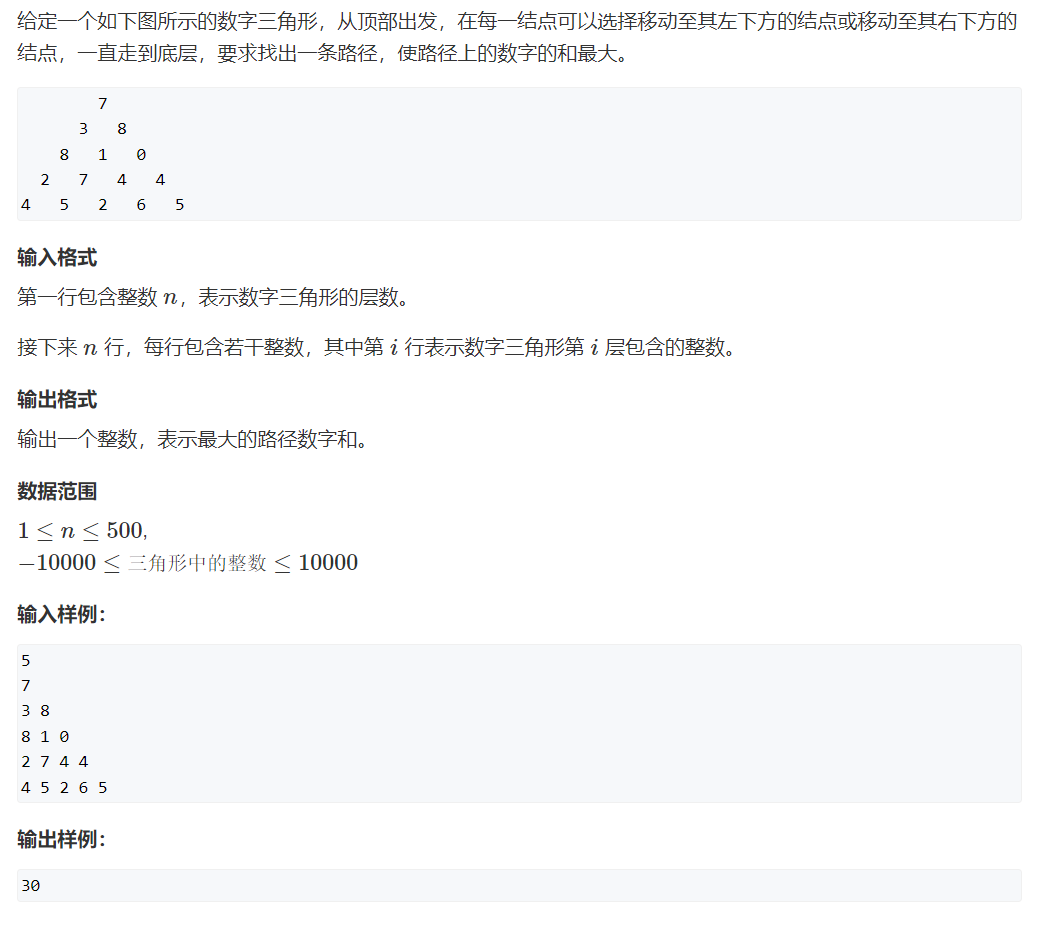
状态分析

我们使用二维数组 a[][] 来存储整个三角形, 使用 f(i, j) 来表示状态: 从底部到点 a[i][j] 的所有路径的集合; 状态属性为: MAX.

点 a[i][j] 只能从 a[i + 1][j] 或者 a[i + 1][j + 1] 处到达, 因此状态转移方程为:

f(i, j) = max(f(i + 1, j), f(i + 1, j + 1)) + a[i][j]

注意: 如果从上往下递推, 会导致需要判断边界; 而从下往上递推不需要判断.

从下往上递推:

public class acwing_898 {

    static final int N = 510;
    static int[][] f = new int[N][N];
    static int[][] a = new int[N][N];

    static int n;

    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

    public static void main(String[] args) throws IOException {
        n = Integer.parseInt(reader.readLine());

        for (int i = 0; i < n; i++) {
            String[] nums = reader.readLine().split(" ");

            for (int j = 0; j <= i; j++) {
                a[i][j] = Integer.parseInt(nums[j]);
            }
        }

        for (int i = 0; i < n; i++) {
            f[n - 1][i] = a[n - 1][i];
        }

        for (int i = n - 2; i >= 0; i--) {
            for (int j = 0; j <= i; j++) {
                f[i][j] = Math.max(f[i + 1][j + 1], f[i + 1][j]) + a[i][j];
            }
        }

        System.out.println(f[0][0]);
    }

}

从上往下递推:

public class acwing_898 {

    static final int N = 510;
    static int[][] f = new int[N][N];
    static int[][] a = new int[N][N];
    static int n;

    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

    public static void main(String[] args) throws IOException {
        n = Integer.parseInt(reader.readLine());

        for (int i = 1; i <= n; i++) {
            Arrays.fill(f[i], Integer.MIN_VALUE);
        }

        for (int i = 1; i <= n; i++) {
            String numsStr = reader.readLine();
            String[] nums = numsStr.split(" ");

            for (int j = 1; j <= i; j++) {
                a[i][j] = Integer.parseInt(nums[j - 1]);
            }
        }

        f[1][1] = a[1][1];

        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                f[i][j] = Math.max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];
            }
        }

        int max = Integer.MIN_VALUE;
        for (int i : f[n]) {
            if (max < i) {
                max = i;
            }
        }

        System.out.println(max);
    }
}