最长公共子序列

例题

最长公共子序列-acwing

最长公共子序列-acwing

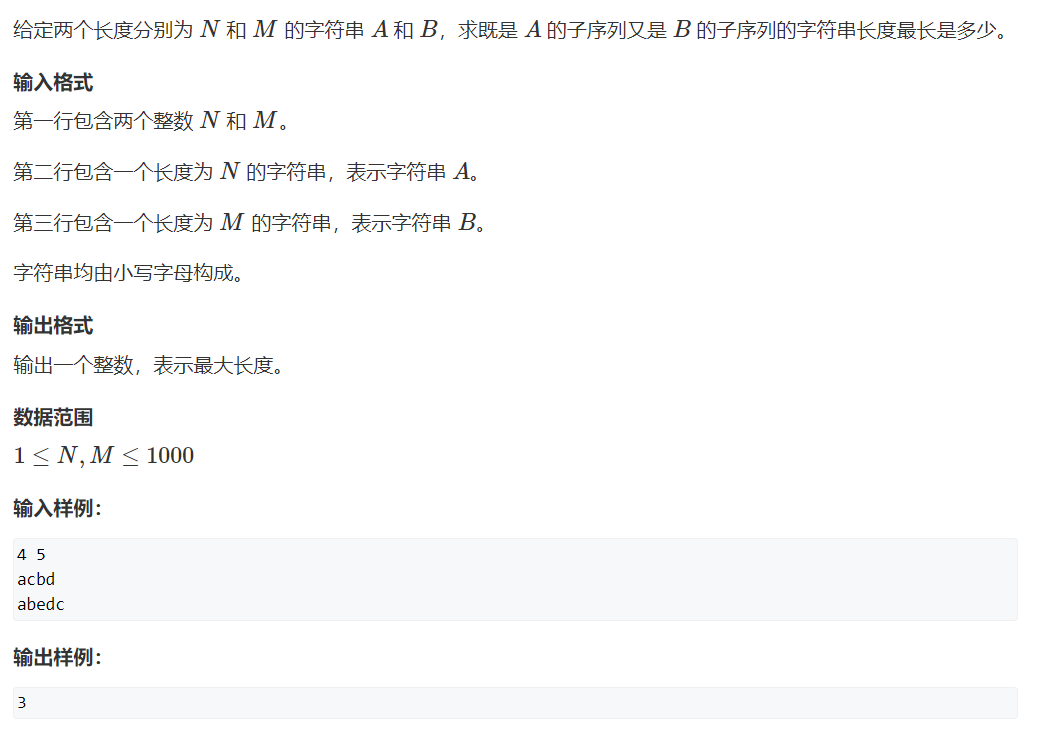
状态分析

这道题状态分析较困难, 主要有两个难点:

1. 状态表示
2. 状态转移

状态表示

f(i, j): A[1 ~ i] 中和 B[1 ~ j] 中所有的公共子序列的集合; 属性为 MAX.

状态转移

f(i, j) 可以划分为由四种状态转移而来:

1. A[i] 和 B[j] 都不取: f(i, j) = f(i - 1, j - 1).
2. 取 A[i] 不取 B[j]: 但是 f(i, j) >= f(i, j - 1), 因为 f(i, j - 1) 包含 A[i], B[j] 都不取, 也包含取 A[i] 不取 B[j].
3. 取 B[j] 不取 A[i]: f(i, j) >= f(i - 1, j), 同上.
4. A[i] 和 B[j] 都取: 此时需要满足 A[i] == B[j], f(i, j) = f(i - 1, j - 1) + 1.

DP 的状态划分应该不重不漏, 但是在计算最大值时, 即使划分的状态重复也不会影响最值, 因此, 可以使用以上划分来进行状态转移计算. 即对于情况(2)(3): f(i, j) = f(i, j - 1), f(i, j) = f(i - 1, j).

同时发现: 情况(2)(3)包含了情况(1), 可以直接舍去情况(1).

public class acwing_897 {

    static int N = 1010;
    static int[][] f = new int[N][N];

    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));

    public static void main(String[] args) throws IOException {
        String[] nums = reader.readLine().split(" ");
        int n = Integer.parseInt(nums[0]);
        int m = Integer.parseInt(nums[1]);

        String s1 = reader.readLine();
        String s2 = reader.readLine();

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                f[i][j] = Math.max(f[i - 1][j], f[i][j - 1]);

                if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
                    f[i][j] = Math.max(f[i][j], f[i - 1][j - 1] + 1);
                }
            }
        }

        System.out.println(f[n][m]);
    }
}